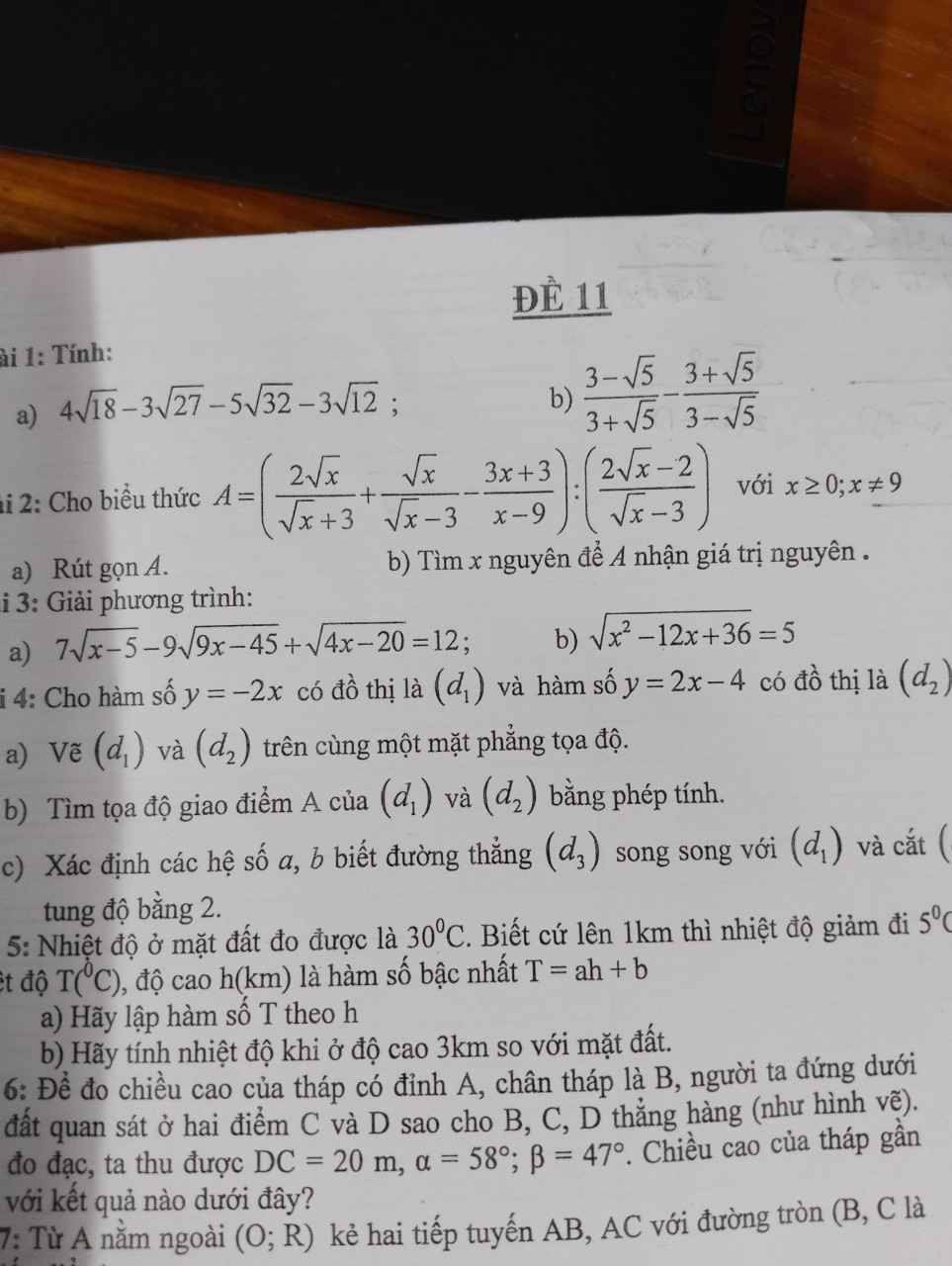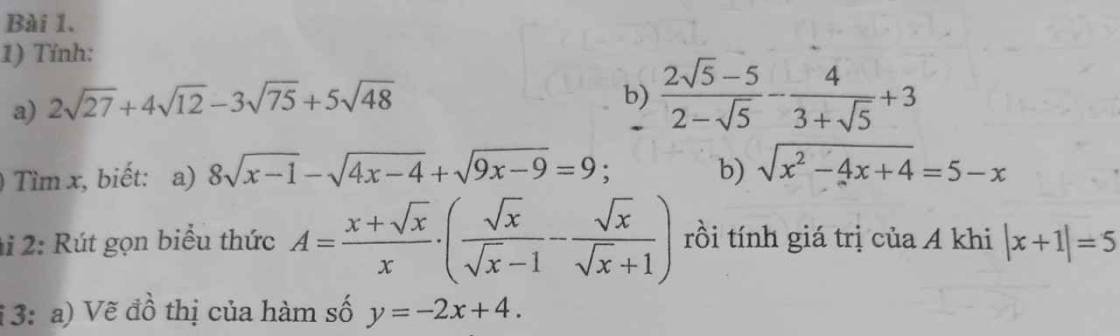Bài 2:
a: \(A=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right):\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}\)
\(=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right)\cdot\dfrac{\sqrt{x}-3}{2\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{2\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\sqrt{x}+3}\cdot\dfrac{1}{2\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{1}{2\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-3\sqrt{x}-3}{2\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)