Giả sử \(a;b;c\) đều là số lẻ
\(\Rightarrow a^2+b^2+c^2-2abc\) sẽ lẻ
\(\Rightarrow a^2+b^2+c^2-2abc\)\(⋮̸\)\(6\) trái với đề bài
\(\Rightarrow\) Trong 3 số \(a;b;c\) phải có ít nhất 1 số chẵn
\(\Rightarrow abc⋮2\)
Giả sử \(abc\)\(⋮̸\)\(3\) có nghĩa là trong 3 số \(a;b;c\) không có số nào chia hết cho \(3\)
\(\Rightarrow a^2\equiv b^2\equiv c^2\equiv1\left(mod3\right)\)
mà \(a^2+b^2+c^2-2abc⋮3\)
\(\Rightarrow-2abc⋮3\) vô lý vì \(a;b;c\) đều không chia hết cho \(3\)
\(\Rightarrow abc⋮3\)
Ta thấy khi số chính phương chia cho \(3\) thì có thể dư là \(0;1\)
\(\Rightarrow a^2;b^2;c^2⋮3\)
\(\Rightarrow a;b;c⋮3\)
\(\Rightarrow abc⋮27\)
mà \(\left(27;2\right)=1\)
\(\Rightarrow abc⋮\left(27.2\right)\) hay \(abc⋮54\left(đpcm\right)\)
Bài 7:
Do \(ab-bc-ca⋮3\), nên \(ab-bc-ca\equiv0\left(mod3\right)\)
\(\Rightarrow ab+c^2\equiv c\left(c+a+b\right)\left(mod3\right)\).
Mà \(a+b+c⋮3\), nên \(ab+c^2\equiv0\left(mod3\right)\), hay \(c^2\equiv-ab\left(mod3\right)\)
Mặt khác: \(a+b+c\equiv0\left(mod3\right)\Leftrightarrow c\equiv-\left(a+b\right)\left(mod3\right)\Rightarrow c^2\equiv\left(a+b\right)^2\left(mod3\right)\), nên:
\(\left(a+b\right)^2\equiv-ab\left(mod3\right)\Rightarrow a^2+b^2+3ab\equiv0\left(mod3\right)\Rightarrow a^2+b^2\equiv0\left(mod3\right)\).
Như vậy, \(a^2+b^2⋮3\), điều này chỉ xảy ra khi và chỉ khi \(a,b⋮3\). Khi đó \(c⋮3\). Từ đây suy ra điều cần chứng minh.








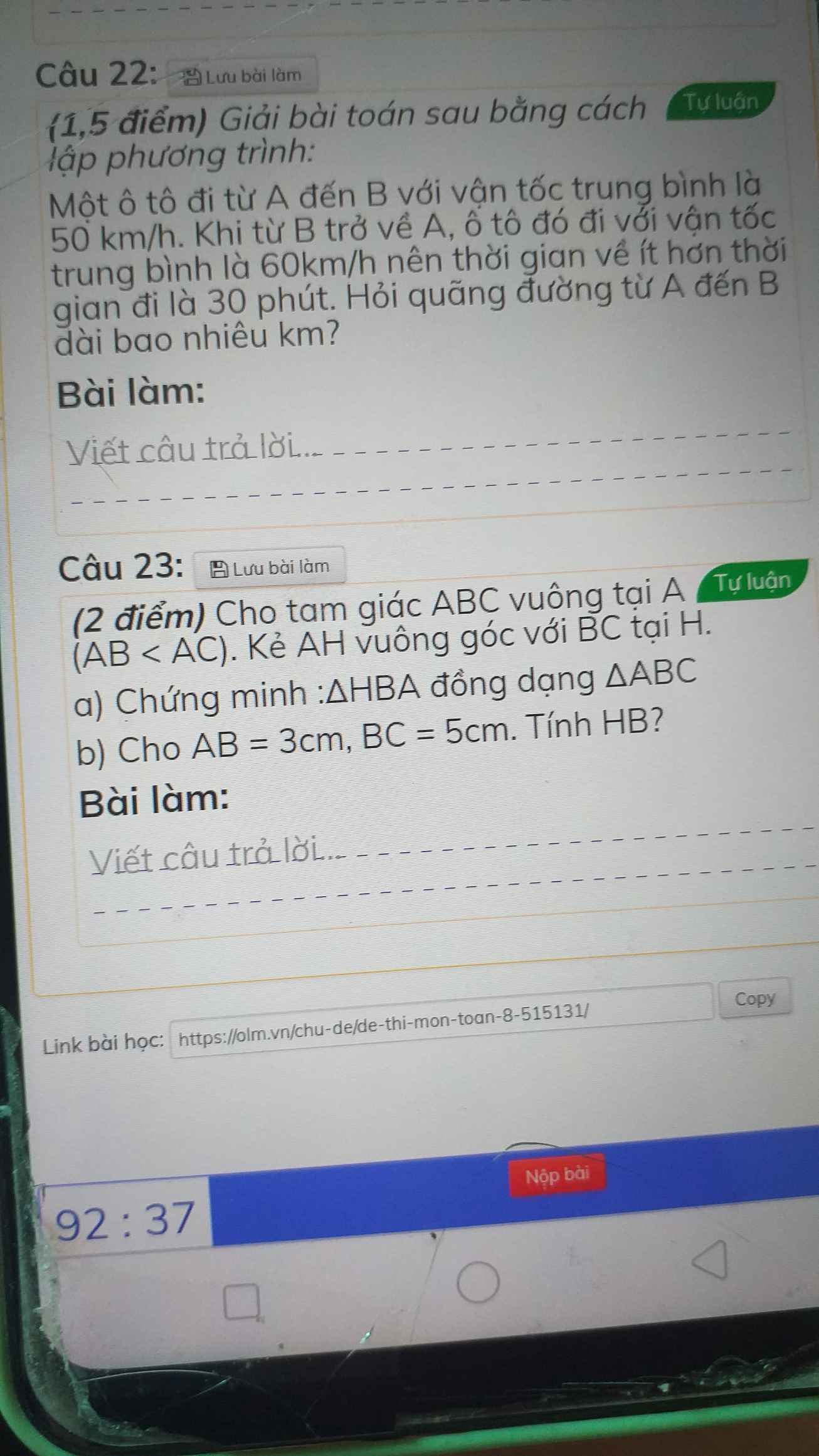
 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
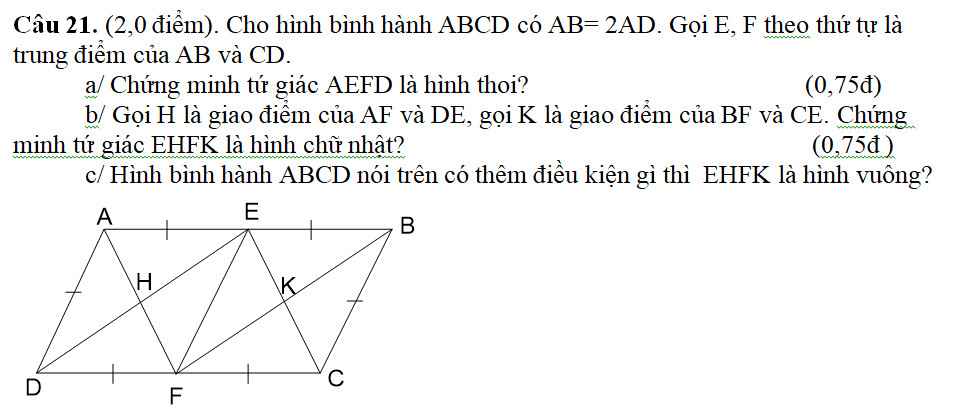
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
 giúp em bài này vs ạ em cảm ơn trc ạ
giúp em bài này vs ạ em cảm ơn trc ạ
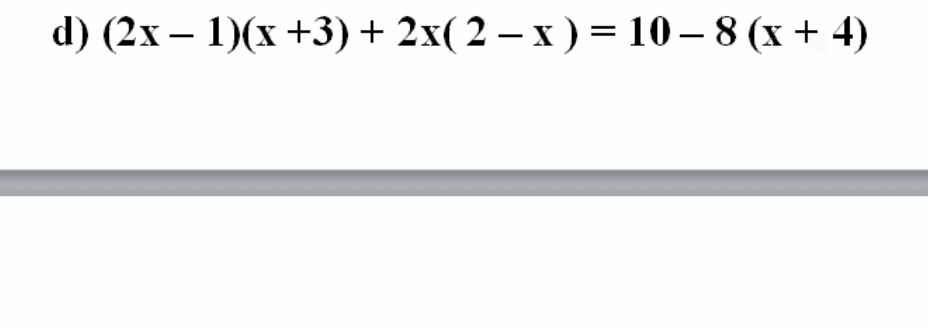 Giúp em vs ạ ! Em camon.
Giúp em vs ạ ! Em camon.