Question

giúp e với ạ e đang cần gấp cảm ơn mọi người nhiều :(

Cho tam giác ABC nhọn có 2 đường cao BE và CF cắt nhau tại H.

a)  Chứng minh tam giác BHF đồng dạng với tam giác CHE và suy ra HE.HB=HC.HF

b) Chứng minh tam giác AEF đồng dạng với tam giác ABC

Answer 1

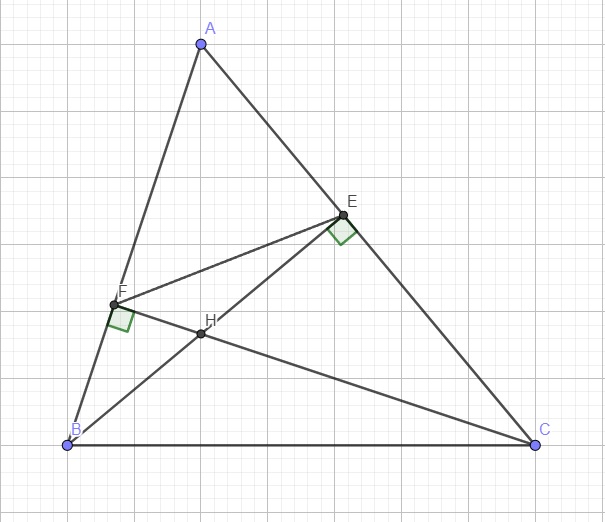
a.

Do BE, CF là các đường cao \(\Rightarrow\widehat{BFH}=\widehat{CEH}=90^0\)

Xét hai tam giác BHF và CHE có:

\(\left\{{}\begin{matrix}\widehat{BFH}=\widehat{CEH}=90^0\\\widehat{BHF}=\widehat{CHE}\left(\text{đối đỉnh}\right)\end{matrix}\right.\) 

\(\Rightarrow\Delta BHF\sim\Delta CHE\left(g.g\right)\)

\(\Rightarrow\dfrac{HB}{HC}=\dfrac{HF}{HE}\Rightarrow HE.HB=HC.HF\)

b.

Xét hai tam giác BAE và CAF có:

\(\left\{{}\begin{matrix}\widehat{A}-chung\\\widehat{BEA}=\widehat{CFA}=90^0\end{matrix}\right.\)

\(\Rightarrow\Delta BAE\sim\Delta CAF\left(g.g\right)\)

\(\Rightarrow\dfrac{AE}{AF}=\dfrac{AB}{AC}\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

Xét hai tam giác AEF và ABC có:

\(\left\{{}\begin{matrix}\widehat{A}-chung\\\dfrac{AE}{AB}=\dfrac{AF}{AC}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\)

Answer 2

Answer 3

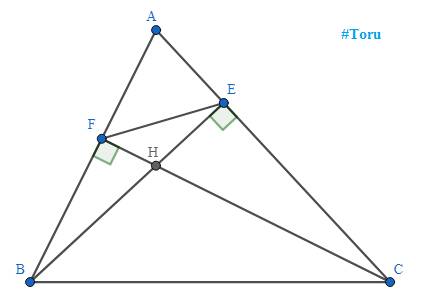
a) Xét \(\Delta BHF\) và \(\Delta CHE\) có:

\(\left\{{}\begin{matrix}\widehat{BFH}=\widehat{CEH}=90^{\circ}\left(CF\bot AB;BE\bot AC;BE\cap CF=\left\{H\right\}\right)\\\widehat{BHF}=\widehat{CHE}\left(\text{hai góc đối đỉnh}\right)\end{matrix}\right.\)

\(\Rightarrow \Delta BHF\backsim \Delta CHE\) \(\left(g.g\right)\Rightarrow\dfrac{HB}{HC}=\dfrac{HF}{HE}\) (các cạnh tương ứng)

\(\Rightarrow HE\cdot HB=HC\cdot HF\) (đpcm)

b) Xét \(\Delta ABE\) và \(\Delta ACF\) có: \(\left\{{}\begin{matrix}\widehat{AEB}=\widehat{AFC}=90^{\circ}\left(BE\bot AC;CF\bot AB\right)\\\widehat{BAC}\text{ chung}\end{matrix}\right.\)

\(\Rightarrow \Delta ABE \backsim \Delta ACF\) \(\left(g.g\right)\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AF}\) (các cạnh tương ứng)

\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

Xét \(\Delta AEF\) và \(\Delta ABC\) có: \(\left\{{}\begin{matrix}\dfrac{AE}{AB}=\dfrac{AF}{AC}\left(cmt\right)\\\widehat{BAC}\text{ chung}\end{matrix}\right.\)

\(\Rightarrow \Delta AEF \backsim \Delta ABC\) \(\left(c.g.c\right)\) (đpcm)

\(\text{#}Toru\)