b) \(B=\left(x^3-3x^2y+3xy^2-y^3\right)-6\left(x^2-2xy+y^2\right)+12\left(x-y\right)-8\)
\(B=\left(x-y\right)^3-6\left(x-y\right)^2+12\left(x-y\right)-8\)
\(B=\left(x-y\right)^3-3\cdot2\cdot\left(x-y\right)^2+3\cdot2^2\cdot\left(x-y\right)-2^3\)
\(B=\left[\left(x-y\right)-2\right]^3\)
\(B=\left(x-y-2\right)^3\)
f) \(F=\left(8x^3+12x^2y+6xy^2+y^3\right)+3\left(4x^2+4xy+y^2\right)y+3\left(2x+y\right)y^2+y^3\)
\(F=\left(2x+y\right)^3+3\left(2x+y\right)^2y+3\left(2x+y\right)y^2+y^3\)
\(F=\left[\left(2x+y\right)+y\right]^3\)
\(F=\left(2x+y+y\right)^3\)
\(F=\left(2x+2y\right)^3\)
b: =(x-y)^3-6(x-y)^2+12(x-y)-2^3
=(x-y-2)^3
f: =(2x+y)^3+3(2x+y)^2*y+3*(2x+y)*y^2+y^3
=(2x+y+y)^3
=(2x+2y)^3
`a, = (x+1)^3 + 3(x+1)^2y + 3(x+1)y^2 + y^3`
`= (x+1+y)^3`
`= x^3 + 1 + y^3 + 3(x+1)(y+1)(xy)`
`= x^3 + y^3 + 1 + 3x^2y^2 + 3x^2y + 3xy^2 + 3xy`
`D=(x-y-1)^3-(x-y+1)^3+6(x-y)^2`
Đặt `x-y=c`
`=(c−1)^3−(a+1)^3+6a^2`
`=c^3−3c^2+3c−1−c^3−3c^2−3c−1+6c^2`
`=-2`
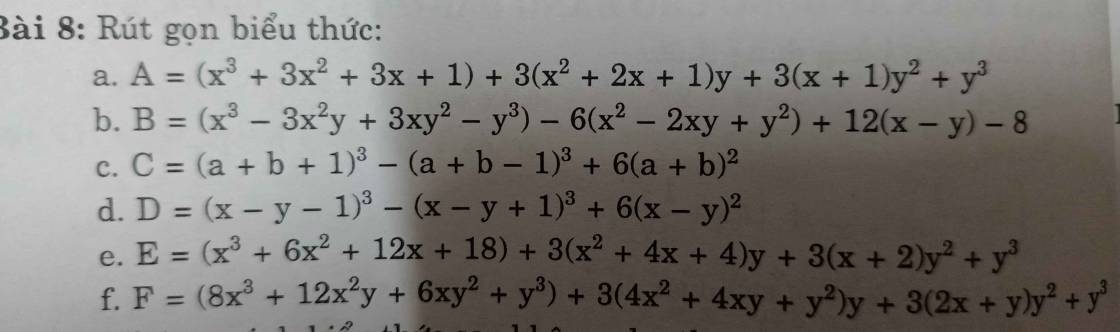
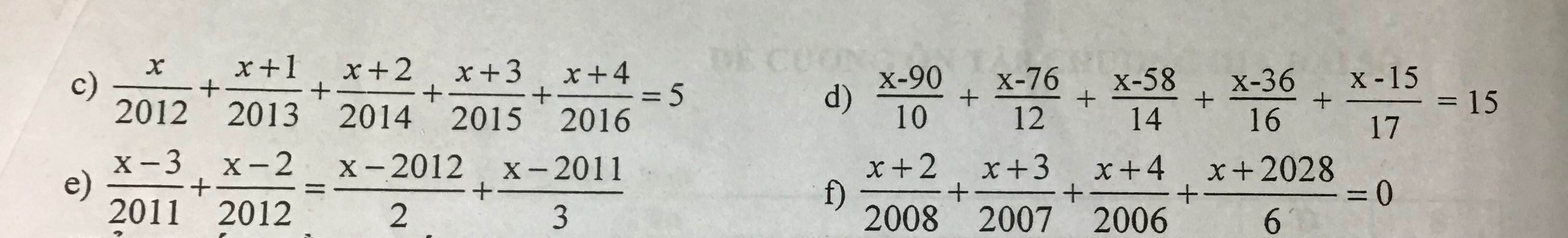Giúp mình d,e,f với ạ !!!! Mình cảm ơn