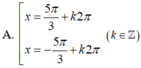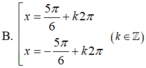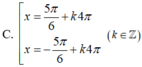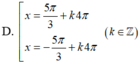1: \(sin2x\cdot sin6x-cos2x\cdot cos6x=\sqrt{3}\cdot sin3x\cdot cos8x\)
=>\(cos2x\cdot cos6x-sin2x\cdot sin6x=-\sqrt{3}\cdot sin3x\cdot cos8x\)
=>\(cos\left(2x+6x\right)=-\sqrt{3}\cdot sin3x\cdot cos8x\)
=>\(cos8x\left(1+\sqrt{3}\cdot sin3x\right)=0\)
=>\(\left[{}\begin{matrix}cos8x=0\\\sqrt{3}\cdot sin3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}8x=\dfrac{\Omega}{2}+k\Omega\\sin3x=-\dfrac{1}{\sqrt{3}}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{16}+\dfrac{k\Omega}{8}\\3x=arcsin\left(-\dfrac{1}{\sqrt{3}}\right)+k2\Omega\\3x=\Omega-arcsin\left(-\dfrac{1}{\sqrt{3}}\right)+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{16}+\dfrac{k\Omega}{8}\\x=\dfrac{1}{3}\cdot arcsin\left(-\dfrac{1}{\sqrt{3}}\right)+\dfrac{k2\Omega}{3}\\x=\dfrac{\Omega}{3}-\dfrac{1}{3}\cdot arcsin\left(-\dfrac{1}{\sqrt{3}}\right)+\dfrac{k2\Omega}{3}\end{matrix}\right.\)
2: \(sin\left(\dfrac{x}{2}\right)\cdot cos\left(\dfrac{3x}{2}\right)-\dfrac{1}{\sqrt{3}}\cdot sin2x=sin\left(\dfrac{3x}{2}\right)\cdot cos\left(\dfrac{x}{2}\right)\)
=>\(sin\left(\dfrac{x}{2}\right)\cdot cos\left(\dfrac{3x}{2}\right)-cos\left(\dfrac{x}{2}\right)\cdot sin\left(\dfrac{3x}{2}\right)=\dfrac{1}{\sqrt{3}}\cdot sin2x\)
=>\(sin\left(\dfrac{x}{2}-\dfrac{3x}{2}\right)=\dfrac{1}{\sqrt{3}}\cdot sin2x\)
=>\(sin\left(-x\right)=\dfrac{1}{\sqrt{3}}\cdot sin2x\)
=>\(sin2x\cdot\dfrac{1}{\sqrt{3}}+sinx=0\)
=>\(sinx\left(2\cdot cosx\cdot\dfrac{1}{\sqrt{3}}+1\right)=0\)
=>\(\left[{}\begin{matrix}sinx=0\\cosx\cdot\dfrac{2}{\sqrt{3}}+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=-1:\dfrac{2}{\sqrt{3}}=-\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=k\Omega\\x=\pm\dfrac{5}{6}\Omega+k2\Omega\end{matrix}\right.\)
3: \(\dfrac{\sqrt{3}}{2}+sin\left(\dfrac{\Omega}{5}\right)\cdot sin2x=sin\left(\dfrac{3}{10}\Omega\right)\cdot cos2x\)
=>\(sin\left(\dfrac{3}{10}\Omega\right)\cdot cos2x-cos\left(\dfrac{3}{10}\Omega\right)\cdot sin2x=\dfrac{\sqrt{3}}{2}\)
=>\(sin\left(\dfrac{3}{10}\Omega-2x\right)=\dfrac{\sqrt{3}}{2}\)
=>\(\left[{}\begin{matrix}\dfrac{3}{10}\Omega-2x=\dfrac{\Omega}{3}+k2\Omega\\\dfrac{3}{10}\Omega-2x=\Omega-\dfrac{\Omega}{3}+k2\Omega=\dfrac{2}{3}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2x=\dfrac{3}{10}\Omega-\dfrac{\Omega}{3}-k2\Omega=\dfrac{-1}{30}\Omega-k2\Omega\\2x=\dfrac{3}{10}\Omega-\dfrac{2}{3}\Omega-k2\Omega=-\dfrac{11}{30}\Omega-k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{1}{60}\Omega-k\Omega\\x=-\dfrac{11}{60}\Omega-k\Omega\end{matrix}\right.\)