\(\sin^6x+cos^6x=\left(\sin^2x+cos^2x\right)^3-3\cdot\sin^2x\cdot cos^2x\cdot\left(\sin^2x+cos^2x\right)\)
\(=1^3-3\cdot\sin^2x\cdot cos^2x\cdot1=1-3\cdot\sin^2x\cdot cos^2x\)
\(=1-3\cdot\left(\sin x\cdot cosx\right)^2=1-3\cdot\left(\frac12\cdot\sin2x\right)^2=1-\frac34\cdot\sin^22x\)
\(8\cdot\left(\sin^6x+cos^6x\right)-3\sqrt3\cdot cos2x=11-3\sqrt3\cdot\sin4x-9\cdot\sin2x\)
=>\(8\left(1-\frac34\cdot\sin^22x\right)-3\sqrt3\cdot cos2x=11-6\sqrt3\cdot\sin2x\cdot cos2x-9\cdot\sin2x\)
=>\(8-6\cdot\sin^22x-3\sqrt3\cdot cos2x-11+6\sqrt3\cdot\sin2x\cdot cos2x+9\cdot\sin2x=0\)
=>\(-6\cdot\sin^22x+6\sqrt3\cdot\sin2x\cdot cos2x+9\cdot\sin2x-3\sqrt3\cdot cos2x-3=0\)
=>\(-2\cdot\sin^22x+2\sqrt3\cdot\sin2x\cdot cos2x+3\cdot\sin2x-\sqrt3\cdot cos2x-1=0\)
=>\(-2\cdot\sin^22x+3\cdot\sin2x-1=\sqrt3\cdot cos2x\cdot\left(1-2\sin2x\right)\)
=>\(-2\cdot\sin^22x+2\cdot\sin2x+\sin2x-1=\sqrt3\cdot cos2x\cdot\left(1-2\sin2x\right)\)
=>\(2\cdot\sin^22x-2\cdot\sin2x-\sin2x+1=\sqrt3\cdot cos2x\cdot\left(2\sin2x-1\right)\)
=>\(\left(\sin2x-1\right)\cdot\left(2\cdot\sin2x-1\right)-\sqrt3\cdot cos2x\cdot\left(2\sin2x-1\right)=0\)
=>\(\left(2\sin2x-1\right)\left(\sin2x-\sqrt3\cdot cos2x-1\right)=0\)
TH1: 2sin 2x-1=0
=>2sin 2x=1
=>\(\sin2x=\frac12\)
=>\(\left[\begin{array}{l}2x=\frac{\pi}{6}+k2\pi\\ 2x=\pi-\frac{\pi}{6}+k2\pi=\frac56\pi+k2\pi\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{\pi}{12}+k\pi\\ x=\frac{5}{12}\pi+k\pi\end{array}\right.\)
TH2: \(\sin2x-\sqrt3\cdot cos2x-1=0\)
=>\(\sin2x-\sqrt3\cdot cos2x=1\)
=>\(\frac12\cdot\sin2x-\frac{\sqrt3}{2}\cdot cos2x=\frac12\)
=>\(\sin\left(2x-\frac{\pi}{3}\right)=\frac12\)
=>\(\left[\begin{array}{l}2x-\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\ 2x-\frac{\pi}{3}=\pi-\frac{\pi}{6}+k2\pi=\frac56\pi+k2\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=\frac{\pi}{6}+\frac{\pi}{3}+k2\pi=\frac{\pi}{2}+k2\pi\\ 2x=\frac56\pi+\frac{\pi}{3}+k2\pi=\frac76\pi+k2\pi\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{\pi}{4}+k\pi\\ x=\frac{7}{12}\pi+k\pi\end{array}\right.\)

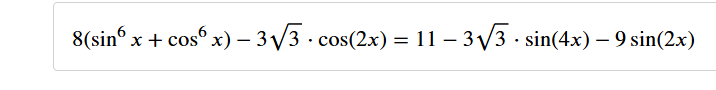 giải phương trình lượng giác sau:
giải phương trình lượng giác sau:











