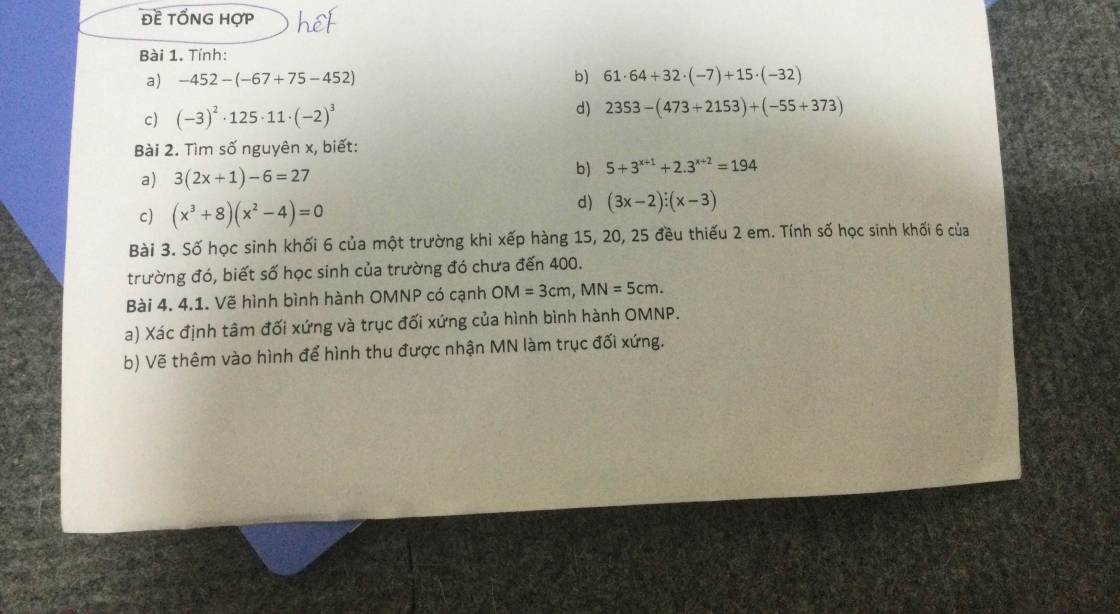Bài 2:
a: \(3\left(2x+1\right)-6=27\)
=>\(3\left(2x+1\right)=33\)
=>\(2x+1=\dfrac{33}{3}=11\)
=>2x=11-1=10
=>\(x=\dfrac{10}{2}=5\)
b: \(5+3^{x+1}+2\cdot3^{x+2}=194\)
=>\(5+3^x\cdot3+2\cdot3^x\cdot9=194\)
=>\(21\cdot3^x=189\)
=>\(3^x=9\)
=>x=2
c: \(\left(x^3+8\right)\left(x^2-4\right)=0\)
=>\(\left[{}\begin{matrix}x^3+8=0\\x^2-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^3=-8\\x^2=4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-2\\x=2\\x=-2\end{matrix}\right.\Leftrightarrow x\in\left\{2;-2\right\}\)
d: \(3x-2⋮x-3\)
=>\(3x-9+7⋮x-3\)
=>\(7⋮x-3\)
=>\(x-3\in\left\{1;-1;7;-7\right\}\)
=>\(x\in\left\{4;2;10;-4\right\}\)
Bài 3:
Gọi số học sinh khối 6 là x(bạn)
(Điều kiện: \(x\in Z^+\))
\(15=3\cdot5;20=2^2\cdot5;25=5^2\)
=>\(BCNN\left(15;20;25\right)=5^2\cdot3\cdot2^2=300\)
Vì số học sinh khi xếp hàng 15;20;25 đều thiếu 2 người
nên ta có: \(x+2\in BC\left(15;20;25\right)\)
=>\(x+2\in B\left(300\right)\)
=>\(x+2\in\left\{300;600;...\right\}\)
=>\(x\in\left\{298;598;...\right\}\)
mà x<400
nên x=298(nhận)
Vậy: Khối 6 có 298 bạn
Bài 1
a) \(-452-\left(-67+75-452\right)\)
\(=-452+67-75+452\)
\(=\left(-452+452\right)+\left(67-75\right)\)
\(=0-8\)
\(=-8\)
b) \(61.64+32.\left(-7\right)+15.\left(-32\right)\)
\(=61.32.2-32.7-32.15\)
\(=32.\left(61.2-7-15\right)\)
\(=32.\left(122-22\right)\)
\(=32.100\)
\(=3200\)
c) \(\left(-3\right)^2.125.11.\left(-2\right)^3\)
\(=9.125.11.\left(-8\right)\)
\(=\left(9.11\right).\left[125.\left(-8\right)\right]\)
\(=99.\left(-1000\right)\)
\(=-99000\)
d) \(2353-\left(473+2353\right)+\left(-55+373\right)\)
\(=2353-473-2353-55+373\)
\(=\left(2353-2353\right)-\left(473-373\right)-55\)
\(=0-100-55\)
\(=-155\)
Bài 2
a) \(3\left(2x+1\right)-6=27\)
\(3\left(2x+1\right)=27+6\)
\(3\left(2x+1\right)=33\)
\(2x+1=33:3\)
\(2x+1=11\)
\(2x=11-1\)
\(2x=10\)
\(x=\dfrac{10}{2}\)
\(x=5\)
b) \(5+3^{x+1}+2.3^{x+2}=194\)
\(3^{x+1}.\left(1+2.3\right)=194-5\)
\(3^{x+1}.7=189\)
\(3^{x+1}=\dfrac{189}{7}\)
\(3^{x+1}=27\)
\(3^{x+1}=3^3\)
\(x+1=3\)
\(x=3-1\)
\(x=2\)
c) \(\left(x^3+8\right)\left(x^2-4\right)=0\)
\(\Rightarrow x^3+8=0;x^2-4=0\)
*) \(x^3+8=0\)
\(x^3=-8\)
\(x^3=\left(-2\right)^3\)
\(x=-2\)
*) \(x^2-4=0\)
\(x^2=4\)
\(x=-2;x=2\)
Vậy \(x=-2;x=2\)
d) \(\left(3x-2\right)⋮\left(x-3\right)\)
\(\Rightarrow\left(3x-9+7\right)⋮\left(x-3\right)\)
\(\Rightarrow\left[3\left(x-3\right)+7\right]⋮\left(x-3\right)\)
\(\Rightarrow7⋮\left(x-3\right)\)
\(\Rightarrow x-3\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow x\in\left\{-4;2;4;10\right\}\)