a) \(\dfrac{1}{3-x}-\dfrac{1}{x+1}=\dfrac{x}{x-3}-\dfrac{\left(x-1\right)^2}{x^2-2x-3}\left(x\ne-1;x\ne3\right)\)
\(\Leftrightarrow\dfrac{1}{3-x}-\dfrac{1}{x+1}=\dfrac{x}{x-3}-\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{-x-1-x+3}{\left(x+1\right)\left(x-3\right)}=\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\left(x-1\right)^2=-2x+2\)
\(\Leftrightarrow x^2-2x+1=-2x+2\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
vì \(x=-1\) không thỏa điều kiện nên nghiệm của phương trình là \(x=1\)
b) \(\dfrac{1}{x-2}-\dfrac{6}{x+3}=\dfrac{5}{6-x^2-x}\left(x\ne-3;x\ne2\right)\)
\(\Leftrightarrow\dfrac{1}{x-2}-\dfrac{6}{x+3}=\dfrac{5}{-\left(x-2\right)\left(x+3\right)}\)
\(\Leftrightarrow\dfrac{x+3-6x+12}{\left(x-2\right)\left(x+3\right)}=\dfrac{-5}{\left(x-2\right)\left(x+3\right)}\)
\(\Leftrightarrow-5x+15=-5\)
\(\Leftrightarrow5x=20\)
\(\Leftrightarrow x=4\)
Vậy \(x=4\) là nghiệm phương trình đã cho
c) \(\dfrac{4x}{x^2+4x+3}-1=6\left(\dfrac{1}{x+3}-\dfrac{1}{2x+2}\right)\left(x\ne-1;x\ne-3\right)\)
\(\Leftrightarrow\dfrac{4x}{\left(x+1\right)\left(x+3\right)}-1=6\left(\dfrac{1}{x+3}-\dfrac{1}{2\left(x+1\right)}\right)\)
\(\Leftrightarrow\dfrac{4x-\left(x+1\right)\left(x+3\right)}{\left(x+1\right)\left(x+3\right)}=3\left(\dfrac{2x+2-x-3}{\left(x+1\right)\left(x+3\right)}\right)\)
\(\Leftrightarrow4x-\left(x^2+4x+3\right)=3\left(x-1\right)\)
\(\Leftrightarrow4x-x^2-4x-3=3x-3\)
\(\Leftrightarrow x^2+3x=0\)
\(\Leftrightarrow x\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\left(ktm\right)\end{matrix}\right.\)
Vậy \(x=0\) là nghiệm của phương trình đã cho

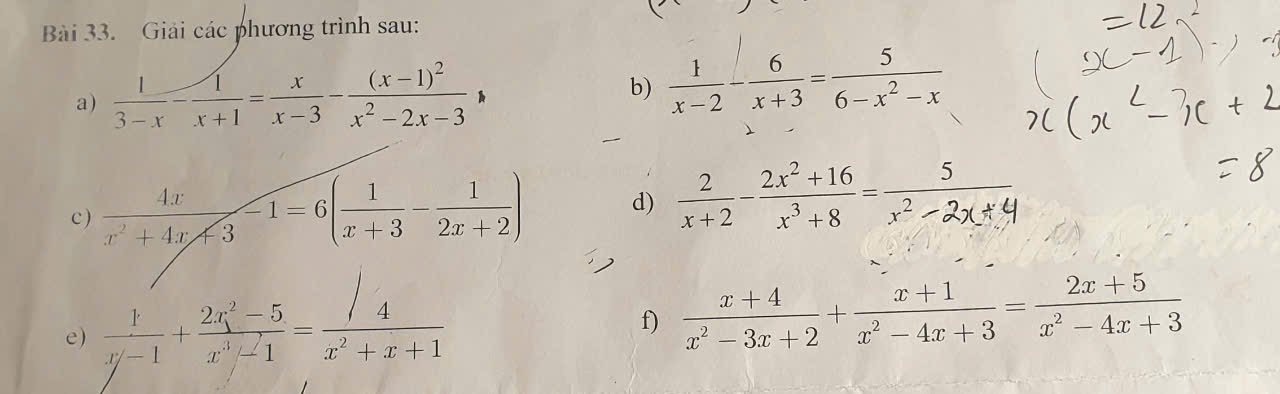 giải giúp mình hết bài 33 với ạ
giải giúp mình hết bài 33 với ạ







 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
 giải giúp mình từ bài 55-bài 58 với ạ.
giải giúp mình từ bài 55-bài 58 với ạ.