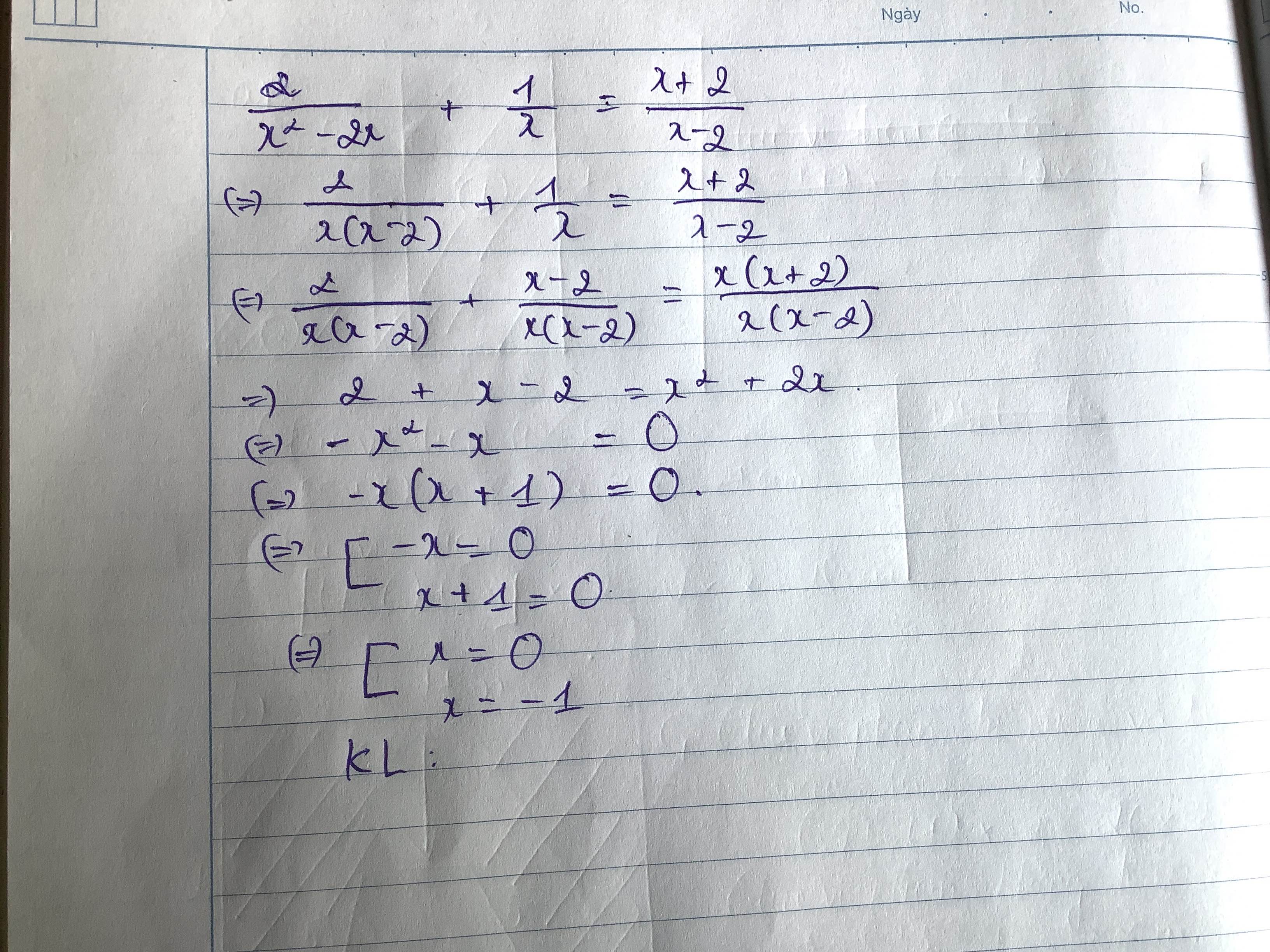Question

 giải các phương trình sau 

\(\dfrac{2}{x^2-2x}+\dfrac{1}{x}=\dfrac{x+2}{x-2}\)

Answer 1

đkxđ \(x\ne0;2\)

\(\dfrac{2}{x^2-2x}+\dfrac{1}{x}=\dfrac{x+2}{x-2}\\ \Leftrightarrow\dfrac{2+\left(x-2\right)-\left(x+2\right)x}{x\left(x-2\right)}=0\\ \Leftrightarrow\dfrac{-x^2-x}{x\left(x-2\right)}=0\\ \Leftrightarrow-x^2-x=0\\ \Leftrightarrow-x\left(x+1\right)=0\)

mà \(x\ne0\Rightarrow x+1=0\\ \Leftrightarrow x=-1\)

Answer 2

Answer 3

=2/x(x-2) + x-2/x(x-2)=x(x+2)/x(x-2)

<=>2 +x +2 -x^2 -2x=0

<=>4 -x -x^2=0

<=>-x(1+x)=4

Answer 4

Ta có: \(\dfrac{2}{x^2-2x}+\dfrac{1}{x}=\dfrac{x+2}{x-2}\)

\(\Leftrightarrow2+x-2=x\left(x+2\right)\)

\(\Leftrightarrow x^2+2x-x=0\)

\(\Leftrightarrow x^2+x=0\)

hay x=-1