9: \(\int\dfrac{x^2-x+4}{x^3-3x^2+2x}dx\)
\(=\int\dfrac{\left(x-1\right)\cdot x+4}{x\left(x-1\right)\left(x-2\right)}dx=\int\left(\dfrac{1}{x-2}+\dfrac{4}{x\left(x-1\right)\left(x-2\right)}\right)dx\)
\(=\dfrac{1}{\left|x-2\right|}+\int\dfrac{4}{x\left(x-1\right)\left(x-2\right)}dx\)
Đặt \(\dfrac{4}{x\left(x-1\right)\left(x-2\right)}=\dfrac{A}{x}+\dfrac{B}{x-1}+\dfrac{C}{x-2}\)
=>\(\dfrac{4}{x\left(x-1\right)\left(x-2\right)}=\dfrac{A\left(x^2-3x+2\right)+B\left(x^2-2x\right)+C\left(x^2-x\right)}{x\left(x-1\right)\left(x-2\right)}\)
=>\(x^2\left(A+B+C\right)+x\left(-3A-2B-C\right)+2A=4\)
=>\(\left\{{}\begin{matrix}A+B+C=0\\-3A-2B-C=0\\2A=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=2\\B+C=-A=-2\\3A+2B+C=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}A=2\\B+C=-2\\2B+C=-3A=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=2\\B=-4\\C=2\end{matrix}\right.\)
=>\(\dfrac{4}{x\left(x-1\right)\left(x-2\right)}=\dfrac{2}{x}+\dfrac{-4}{x-1}+\dfrac{2}{x-2}\)
=>\(\int\dfrac{4}{x\left(x-1\right)\left(x-2\right)}dx=\dfrac{2}{\left|x\right|}+\dfrac{-4}{\left|x-1\right|}+\dfrac{2}{\left|x-2\right|}\)
=>\(\int\dfrac{x^2-x+4}{x^3-3x^2+2x}dx=\dfrac{1}{\left|x-2\right|}+\dfrac{2}{\left|x\right|}+\dfrac{-4}{\left|x-1\right|}+\dfrac{2}{\left|x-2\right|}=\dfrac{3}{\left|x-2\right|}+\dfrac{2}{\left|x\right|}-\dfrac{4}{\left|x-1\right|}\)
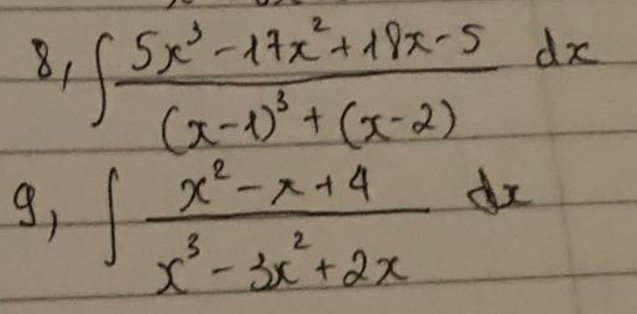
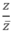là một số thuần ảo. Kết luận nào sau đây là đúng?
