Chọn B.
Đặt
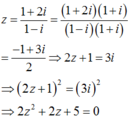
Điều này chứng tỏ z là một nghiệm (phức) của phương trình 2 x 2 + 2 x + 5 = 0
Từ đó suy ra
![]()
Chọn B.
Đặt
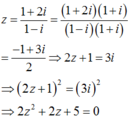
Điều này chứng tỏ z là một nghiệm (phức) của phương trình 2 x 2 + 2 x + 5 = 0
Từ đó suy ra
![]()
Phương trình log 2 x - x 2 - 1 log 3 x + x 2 - 1 = log 6 x - x 2 - 1 có một nghiệm bằng 1 và một nghiệm còn lại dạng x = 1 2 a log b c + a - log b c , trong đó a, b, c là các số nguyên dương và a, c là các số nguyên tố và a > c. Giá trị biểu thức a 2 - 2 b + 3 c bằng
A. 0
B. 3.
C. 6.
D. 4.
Cho phương trình z 3 + a z 2 + b z + c = 0 . Nếu z = 1 − i và z = 1 là hai nghiệm của phương trình thì a − b − c bằng (a, b, c là số thực).
A. 2
B. 3
C. 5
D. 6
Gọi A,B,C là các điểm biểu diễn số phức z 1 , z 2 , z 3 là nghiệm của phương trình z z − 1 − 2 i z − 2 + i = 0 . Tính diện tích S của tam giác ABC.
A. 3 2
B. 5
C. 5 2
D. 2
Cho a,b,c là các số thực sao cho phương trình z 3 + a z 2 + b z + c = 0 có ba nghiệm phức lần lượt là z 1 = ω + 3 i ; z 2 = ω + 9 i ; z 3 = 2 ω - 4 , trong đó ω là một số phức nào đó. Tính giá trị của P=|a+b+c|.
A. P=36
B. P=136
C. P=208
D. P=84
Phương trình 5 x 2 − 3 x + 2 = 3 x − 2 có 1 nghiệm dạng x = log a b với a, b là các số nguyên dương lớn hơn 4 và nhỏ hơn 16. Khi đó a + 2 b bằng
A. 35
B. 30
C. 40
D. 25
Phương trình 5 x 2 - 3 x + 2 = 3 x - 2 có 1 nghiệm dạng x = log a b với a, b là các số nguyên dương lớn hơn 4 và nhỏ hơn 16. Khi đó a+2b bằng
A. 35
B. 30
C. 40
D. 25
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Số thực m nhỏ nhất để phương trình 8 x + 3 x . 4 x + ( 3 x 2 + 1 ) 2 x = ( m 3 - 1 ) x 3 + ( m - 1 ) x có nghiệm dương là a+e lnb, với a,b là các số nguyên. Giá trị của biểu thức a+b bằng
A. 7.
B. 4.
C. 5.
D. 3.
Biết số phức z 1 = 1 + i v à z 2 là hai nghiệm của phương trình z 2 + b z + c = 0 (b,c là các số thực). Khi đó môdun của số phức w = z 1 ¯ − 2 i + 1 z 2 ¯ − 2 i + 1 là
A. w = 63 .
B. w = 65 .
C. w = 8.
D. w = 1.