Các câu hỏi tương tự
Cho hai số phức z;
ω
thỏa mãn
z
-
1
z
+
3
-
2
i
;
ω
z
+
m
+
i
với
m
∈
R
là tham số. Giá trị của m để ta luôn có
ω
≥...
Đọc tiếp
Cho hai số phức z; ω thỏa mãn z - 1 = z + 3 - 2 i ; ω = z + m + i với m ∈ R là tham số. Giá trị của m để ta luôn có ω ≥ 2 5 là
A. m ≥ 7 m ≤ 3
B. m ≥ 7 m ≤ - 3
C. - 3 ≤ m < 7
D. 3 ≤ m ≤ 7
Cho số phức z thỏa mãn
(
2
−
3
i
)
z
+
(
4
+
i
)
z
¯
+
(
1
+
3
i
)
2
0
. Gọi a, b lần lượt là phần thực và phần ảo của số phức z. Khi đó
2
a
-
...
Đọc tiếp
Cho số phức z thỏa mãn ( 2 − 3 i ) z + ( 4 + i ) z ¯ + ( 1 + 3 i ) 2 = 0 . Gọi a, b lần lượt là phần thực và phần ảo của số phức z. Khi đó 2 a - 3 b bằng
A. 1
B. 4
C. 11
D. -19
Cho các số phức z thỏa mãn z - 1 = 5 . Biết rằng tập hợp điểm biểu diễn số phức ω = i z + 1 - i là đường tròn. Tính bán kính r của đường tròn đó.
A. r = 5
B. r = 2
C. r = 4
D. r = 5
Xét số phức z có phần thực dương và ba điểm A,B,C lần lượt là điểm biểu diễn của các số phức
z
,
1
z
và
z
+
1
z
Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của bằng
z
+
1
z
2
A.
2
B. ...
Đọc tiếp
Xét số phức z có phần thực dương và ba điểm A,B,C lần lượt là điểm biểu diễn của các số phức z , 1 z và z + 1 z Biết tứ giác OABC là một hình bình hành, giá trị nhỏ nhất của bằng z + 1 z 2
A. 2
B. 2
C. 2 2
D. 4
Cho số phức z 2 + i.Hãy xác định điểm biểu diễn hình học của số phức
ω
(
1
-
i
)
z
. A. Điểm M B. Điểm N C. Điểm P D. Điểm Q
Đọc tiếp
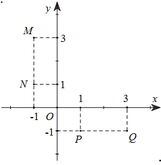
Cho số phức z = 2 + i.
Hãy xác định điểm biểu diễn hình học của số phức ω = ( 1 - i ) z .
A. Điểm M
B. Điểm N
C. Điểm P
D. Điểm Q
Cho a là số thực và z là nghiệm của phương trình
z
2
−
2
z
+
a
2
−
2
a
+
5
0.
Biết
a
a
0
là giá trị để số phức z có môđun nhỏ nhất. Khi đó
a
0
gần giá trị nào nhất trong các giá trị sau? A. -3. B. -1. C. 4. D. 2.
Đọc tiếp
Cho a là số thực và z là nghiệm của phương trình z 2 − 2 z + a 2 − 2 a + 5 = 0. Biết a = a 0 là giá trị để số phức z có môđun nhỏ nhất. Khi đó a 0 gần giá trị nào nhất trong các giá trị sau?
A. -3.
B. -1.
C. 4.
D. 2.
Cho số phức z = a+bi(a,b ϵ ℝ) thỏa mãn |z|=5z và z(2+i)(1-2i) là một số thực. Tính giá trị P=|a|+|b|
A.P=8
B.P=4
C.P=5
D. P=7
Cho số phức z thỏa mãn
z
+
z
¯
+
2
z
-
z
¯
8
; a, b, c dương. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức
P
z
-
3
-
3...
Đọc tiếp
Cho số phức z thỏa mãn z + z ¯ + 2 z - z ¯ = 8 ; a, b, c dương. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P = z - 3 - 3 i . Tính M + m
A. 10 + 34
B. 5 + 58
C. 10 + 58
D. 2 10
Cho số phức z = 1 + 2 i . Điểm nào dưới đây là điểm biểu diễn của số phức ω = z + i z ¯ trong mặt phẳng tọa độ?
A. M(3;3)
B. N(2;3)
C. P(-3;3)
D. Q(3;2)




