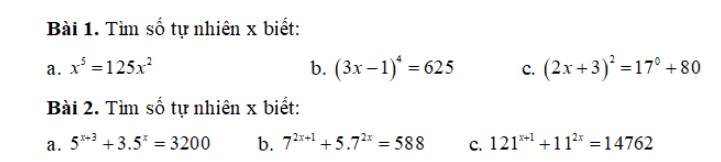Bài 1.
\(a,x^5=125x^2\)
\(\Rightarrow x^5-125x^2=0\)
\(\Rightarrow x^2\left(x^3-125\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x^2=0\\x^3-125=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x^3=125\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^3=5^3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=5\left(tm\right)\end{matrix}\right.\)
Vậy \(x\in\left\{0;5\right\}\).
\(---\)
\(b,\left(3x-1\right)^4=625\)
\(\Rightarrow\left(3x-1\right)^4=\left(\pm5\right)^4\)
\(\Rightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}3x=6\\3x=-4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-\dfrac{4}{3}\left(ktm\right)\end{matrix}\right.\)
Vậy \(x=2\).
\(---\)
\(c,\left(2x+3\right)^2=17^0+80\)
\(\Rightarrow\left(2x+3\right)^2=1+80\)
\(\Rightarrow\left(2x+3\right)^2=81\)
\(\Rightarrow\left(2x+3\right)^2=\left(\pm9\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}2x+3=9\\2x+3=-9\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=6\\2x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-6\left(ktm\right)\end{matrix}\right.\)
Vậy \(x=3\).
Bài 2.
\(a,5^{x+3}+3\cdot5^x=3200\\\Rightarrow 5^x\cdot5^3+5^x\cdot3=3200\\\Rightarrow 5^x\cdot(5^3+3)=3200\\\Rightarrow 5^x\cdot128=3200\\\Rightarrow 5^x=3200:128\\\Rightarrow 5^x=25\\\Rightarrow 5^x=5^2\\\Rightarrow x=2(tm)\)
Vậy \(x=2\).
\(---\)
\(b,7^{2x+1}+5\cdot7^{2x}=588\\\Rightarrow 7^{2x}\cdot7+7^{2x}\cdot5=588\\\Rightarrow 7^{2x}\cdot(7+5)=588\\\Rightarrow 7^{2x}\cdot12=588\\\Rightarrow 7^{2x}=588:12\\\Rightarrow 7^{2x}=49\\\Rightarrow 7^{2x}=7^2\\\Rightarrow 2x=2\\\Rightarrow x=1\)
Vậy \(x=1\).
\(---\)
\(c,121^{x+1}+11^{2x}=14762\\\Rightarrow 121^x\cdot121+(11^2)^x=14762\\\Rightarrow 121^x\cdot121+121^x=14762\\\Rightarrow 121^x\cdot(121+1)=14762\\\Rightarrow 121^x\cdot122=14762\\\Rightarrow 121^x=14762:122\\\Rightarrow 121^x=121\\\Rightarrow x=1(tm)\)
Vậy \(x=1\).
\(Toru\)