Đáp án B.
PT hoành độ giao điểm là
2 x 2 − 2 x + 3 x − 1 = 3 x + 1 ⇔ x ≠ 1 x 2 = 4 ⇒ x = 2 x = − 2 ⇒ A 2 ; 7 B − 2 ; − 5 ⇒ A B = 4 10 .
Đáp án B.
PT hoành độ giao điểm là
2 x 2 − 2 x + 3 x − 1 = 3 x + 1 ⇔ x ≠ 1 x 2 = 4 ⇒ x = 2 x = − 2 ⇒ A 2 ; 7 B − 2 ; − 5 ⇒ A B = 4 10 .
Đường thẳng y = x + 1 cắt đồ thị hàm số y = x + 3 x − 1 tại hai điểm phân biệt A, B. Tính độ dài đoạn thẳng AB.
A. A B = 34
B. A B = 8
C. A B = 6
D. A B = 17
Đường thẳng d : y = x - 3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng D: x-y=0. Tính d = d 1 + d 2
A. d = 3 2
B. d = 3 2 2
C. d = 6
D. d = 2 2
Đồ thị hàm số y = 4 x − 1 x + 4 cắt đường thẳng y = x + 4 tại hai điểm phân biệt A, B. Tìm tọa độ trung điểm C của AB.
A. C(0;4)
B. C(-2;6)
C. C(4;0)
D. C(2;-6)
Khi đồ thị hàm số y = x 3 - 3 m x + 2 có hai điểm cực trị A, B và đường tròn (C): ( x - 1 ) 2 + ( y - 1 ) 2 = 3 cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN
A. MN= 3
B. MN=1.
C. MN=2.
D. MN=2 3
Biết rằng đồ thị (C) của hàm số y = 2 x + 1 x + 2 luôn cắt đường thẳng d : y = - x + m tại hai điểm phân biệt A và B. Tìm các giá trị thực của tham số m sao cho độ dài đoạn thẳng AB ngắn nhất
A. m = 1
B. m = 2 3
C. m = 4
D. m = 0
Tìm giá trị thực của tham số m để đường thẳng d : y = x - m + 2 cắt đồ thị hàm số y = 2 x x - 1 tại hai điểm phân biệt A và B sao cho độ dài AB ngắn nhất.
A. m = - 3
B. m = 3
C. m = - 1
D. m = 1
Cho hàm số y = 2 x - 1 x - 1 có đồ thị ( c ).Tìm tất cảc các giá trị thực của tham số m để đường thẳng: d: y= x +m và cắt ( c ) tại hai điểm phân biệt A, B sao cho AB = 4.
A. m= -1
B. 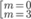
C. 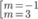
D. m=4
Đồ thị (C) của hàm số y = x + 1 x - 1 và đường thẳng d: y=2x-1 cắt nhau tại hai điểm A và B khi đó độ dài đoạn AB bằng?
A. 2 3
B. 2 2
C. 2 5
D. 5
Có bao nhiêu số nguyên dương m sao cho đường thẳng y = x + m x cắt đồ thị hàm số y = 2 x − 1 x + 1 tại hai điểm phân biệt A, B và A B ≤ 4
A. 7
B. 6
C. 1
D. 2