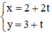Thay x=1 và y=1 vào Δ, ta được:
a+b-3=0
=>a+b=3
=>a=3-b
\(d\left(M;\text{Δ}\right)=\sqrt{5}\)
=>\(\dfrac{\left|a\cdot2+b\cdot3-3\right|}{\sqrt{a^2+b^2}}=\sqrt{5}\)
=>\(\sqrt{5\left(b^2-6b+9+b^2\right)}=\left|2\left(3-b\right)+3b-3\right|\)
=>\(\sqrt{5\left(2b^2-6b+9\right)}=\left|b+3\right|\)
=>10b^2-30b+45=b^2+6b+9
=>9b^2-36b+36=0
=>b^2-4b+4=0
=>b=2 và a=1
=>a-2b=1-4=-3