Theo đề bài ta có V = 18000 c m 3 , h = 40cm
Do đó, ta có:
V = 1 3 πr 2 h ⇒ r = 3 V πh = 3 . 18000 40 π ⇒ r ≈ 20 , 72 cm
Vậy bán kính của hình tròn là r = 21cm
Đáp án D
Theo đề bài ta có V = 18000 c m 3 , h = 40cm
Do đó, ta có:
V = 1 3 πr 2 h ⇒ r = 3 V πh = 3 . 18000 40 π ⇒ r ≈ 20 , 72 cm
Vậy bán kính của hình tròn là r = 21cm
Đáp án D
Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón. một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m (Các kích thước cho trên hình 100). Khi đó diện tích mặt ngoài của dụng cụ (Không tính nắp đậy) có giá trị gần nhất với:
A. 5,58
B.6,13
C. 4,86
D. 6,36
Một phễu gồm một phần có dạng trụ, phần còn lại có dạng nón. Một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m. Khi đó diện tích mặt ngoài của dụng cụ (Không tính nắp đậy) có giá trị gần nhất với:
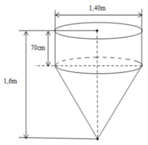
A. 5,58
B. 6,13
C. 4,68
D. 5,53
Cho hình nón có chiều cao h, đường tròn đáy có bán kính R. Một mặt phẳng (P) di động song song với đáy hình nón cắt hình nón theo đường tròn giao tuyến (L). Dựng hình trụ có một đáy là đường tròn (L), một đáy nằm trên đáy hình nón có trục là trục của hình nón. Gọi x là chiều cao của hình trụ, giá trị của x để hình trụ có thể tích lớn nhất
A. x = h 2
B. x = h 3
C. x = h 4
D. x = h
Một cái th ng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của th ng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của th ng, có đ nh là tâm của miệng thùng và có chiều cao bằng 20cm (xem hình minh họa). Biết rằng đổ 4.000 c m 3 nước vào th ng thì đầy th ng (nước không chảy được vào bên trong phễu), tính bán kính đáy r của phễu (giá trị gần đúng của r làm tròn đến hàng phần trăm).
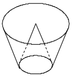
A. r = 9,77 cm
B. r = 7,98 cm
C. r = 5,64 cm
D. r = 5,22 cm
Một bạn học sinh cắt lấy tờ giấy hình tròn (có bán kính R) rồi cắt một phần giấy có dạng hình quạt. Sau đó bạn ấy lấy phần giấy đó làm thành cái nón chú hề (như hình vẽ). Gọi x là chiều dài dây cung tròn của phần giấy được xếp thành nón chú hề, còn h, r lần lượt là chiều cao và bán kính đáy của của cái nón. Nếu x = k . R thì giá trị k xấp xỉ bằng bao nhiêu để thể tích của hình nón là lớn nhất.
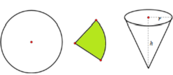
A. 3,15
B. 4,67
C. 5,13
D. 6,35
Một vật N1 có dạng hình nón có chiều cao bằng 40cm. Người ta cắt vật N1 bằng một mặt cắt song song với mặt đáy của nó để được một hình nón nhỏ N2 có thể tích bằng 1 8 thể tích N2.Tính chiều cao h của hình nón N2?
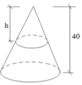
A. 10cm
B. 20cm
C. 40cm
D. 5cm
Cho hình nón tròn xoay có chiều cao h = 20 c m , bán kính đáy r = 25 c m . Mặt phẳng α đi qua đỉnh của hình nón cách tâm của đáy 12cm Tính diện tích thiết diện của hình nón cắt bởi mặt phẳng α
A. S = 400 c m 2
B. S = 406 c m 2
C. S = 300 c m 2
D. S = 500 c m 2
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó, Người ta thả vào đó một khối trụ và đo được thể tích nước tràn ra ngoài là 16 π 3 d m 3 . Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón, các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ có chiều cao bằng đường kính đáy của hình nón. Tính diện tích xung quanh S x q của bình nước
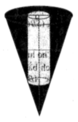
A. 9 π 10 2 d m 2
B. 4 π 10 d m 2
C. 4 π d m 2
D. 2 π d m 2
Một con quay là ghép của 2 khối trụ được xếp chồng lên khối nón. Thiết diện qua trục có dạng như hình vẽ bên. Khối trụ thứ nhất có bán kính đáy r1, chiều cao h1; khối trụ thứ hai có bán kính đáy r2, chiều cao h2; khối nón có bán kính đáy r3, chiều cao h3. Biết rằng r2 = 2r1 = 2r3; h3 = 2h2 = 4h1 và thể tích của con quay bằng 31 c m cubed Thể tích của phần khối nón bằng
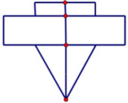
A. 3 c m 3
B. 6 c m 3
C. 8 c m 3
D. 4 c m 3