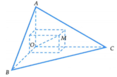
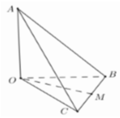
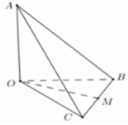
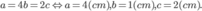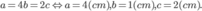Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = 3cm, OB = 6cm, OC = 12cm. Trên mặt (ABC) người ta đánh dấu một điểm M sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện .Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng:
A. 8 c m 3 .
B. 24 c m 3 .
C. 12 c m 3 .
D. 36 c m 3 .
Chọn A.
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó
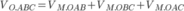
Hay 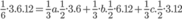

Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có :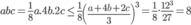 (Theo bất đẳng thức Cô-sin).
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 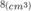 khi
khi