Đáp án C
Yêu cầu bài toán ⇔ x 2 - ( 1 - m ) x + 2 m = 0 có 2 nghiệm phân biệt lớn hơn hoặc bằng -1
Khi và chỉ khi ∆ > 0 x 1 + x 2 + 2 ≥ 0 x 1 + 1 x 2 + 1 ≥ 0 ⇔ 1 - m 2 - 4 . 2 m > 0 1 - m + 2 ≥ 0 2 m + 2 - m + 1 ≥ 0 ⇔ - 2 ≤ m ≤ 5 - 2 6 .
Đáp án C
Yêu cầu bài toán ⇔ x 2 - ( 1 - m ) x + 2 m = 0 có 2 nghiệm phân biệt lớn hơn hoặc bằng -1
Khi và chỉ khi ∆ > 0 x 1 + x 2 + 2 ≥ 0 x 1 + 1 x 2 + 1 ≥ 0 ⇔ 1 - m 2 - 4 . 2 m > 0 1 - m + 2 ≥ 0 2 m + 2 - m + 1 ≥ 0 ⇔ - 2 ≤ m ≤ 5 - 2 6 .
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = 1 + x + 1 x 2 - 1 - m x + 2 m có hai tiệm cận đứng?
A. 0
B. 2
C. 3
D. 1
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1 có hai tiệm cận đứng
A. m ≥ 4
B. − 5 < m ≤ 4
C. m > − 5
D. − 5 < m ≤ 4 m ≠ − 1
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = x 2 x 2 − 2 x − m − x − 1 có hai tiệm cận đứng
A. m ≥ 4
B. − 5 < m ≤ 4
C. m > − 5
D. − 5 < m ≤ 4 m ≠ − 1
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x - 2 x 2 - m x + 1 có hai đường tiệm cận đứng
A. m ∈ ( - ∞ ; - 2 ) ∪ ( 2 ; + ∞ ) \ 5 2
B. m ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
C. m ∈ ( - ∞ ; - 2 ) ∪ ( 2 ; + ∞ )
D. m ≢ 5 2
Cho hàm số y = x - 3 x - m 2 + 1 (m là tham số; m ≠ ± 2 ). Có bao nhiêu giá trị của tham số m để hình phẳng giới hạn bởi hai trục tọa độ và hai đường tiệm cận của đồ thị hàm số đã cho là một hình vuông.
A. 1
B. 3
C. 2
D. 4.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 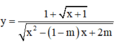 có hai tiệm cận đứng?
có hai tiệm cận đứng?
A. 3
B. 0
C. 2
D. 1
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2019;2019] để đồ thị hàm số y = 2 x + 1 4 x 2 − 2 x + m có hai đường tiệm cận đứng?
A. 2020
B. 4038
C. 2018
D. 2019
Tìm tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = 1 + x + 1 x 2 − m x − 3 m có đúng hai tiệm cận đứng ?
A. − ∞ ; − 12 ∪ 0 ; + ∞
B. 0 ; + ∞
C. 1 4 ; 1 2
D. 0 ; 1 2
Tìm tất cả giá trị của tham số m để đồ thị hàm số y = x - m x 2 - ( m + 1 ) x + m có hai tiệm cận
A. m ≠ 1
B. m ≥ 1
C. m ≤ 1
D. m ∈ ℝ