d) Ta có: \(\left(-a-b\right)^2\)
\(=\left[-\left(a+b\right)\right]^2\)
\(=1\cdot\left(a+b\right)^2=\left(a+b\right)^2\)
e) Ta có: \(\left(x+y\right)^2-4xy\)
\(=x^2+2xy+y^2-4xy\)
\(=y^2-2xy+x^2\)
\(=\left(y-x\right)^2\)
Bài 7: Cho ABC nhọn có các đường cao AD,BE,CF cắt nhau tại H.
a. Chứng minh AB.AF=AC.AE
b. Chứng minh AEF ABC.
c. Chứng minh Góc BEF=BCF
d. Chứng minh BH.BE+CH.CF=BC2.
e. Chứng minh EH là phân giác
g. Chứng minh : AF/FB.DB/DC.CE/EA=1
Cho tam giác nhọn ABC, kẻ đường cao BE và CF cắt nhau tại H 
.
a/ Chứng minh: 
b/ Chứng minh :AB.AF = AE . AC
c/ Chứng minh : AH
BC.
d/ Chứng minh . BH.BE+CH.CF=BC2
Cho tam giác nhọn ABC, các đường cao AD, BE, CF
a. Chứng minh đồng dạng với .
b. Chứng minh AF.AB = AE. AC
c. Chứng minh: ΔAEF = ΔABC
d. Cho AE = 3cm, AB= 6cm. Chứng minh rằng SABC = 4SAEF
chứng minh đối xứng có cần chứng minh thẳng hàng không. Có mấy cách chứng minh đối xứng
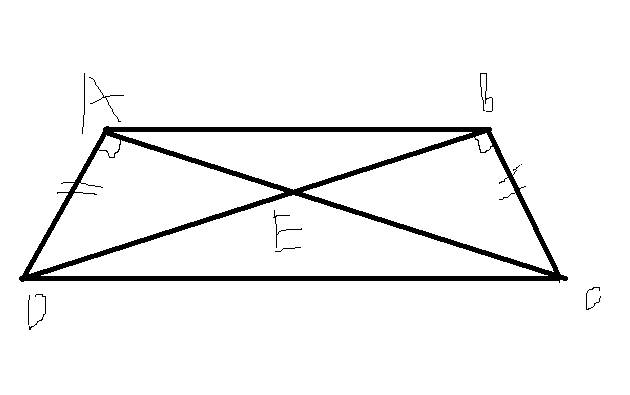
a) Chứng minh tam giác ADC = tam giác BCD
B) Chứng minh tam giác DEC cân
c) Chứng minh AB//CD
Bài 7. Cho ∆ABC nhọn, 3 đường cao AM, BN, CP đồng quy tại H. a) Chứng minh: ∆ABM ∽ ∆AHP và ∆ABH ∽ ∆AMP; b) Chứng minh: MH.MA = MB.MC; c) Chứng minh: ∆AHB ∽ ∆NHM; d) Chứng minh: ∆MAP ∽ ∆MNH
Cho hình bình hành ABCD tâm O. Gọi M, N lần lượt là trung điểm của AB và CD.
a) Chứng minh DN = AM và chứng minh AMND là hình bình hành.
b) Chứng minh MBND là hình bình hành.
c) Chứng minh AN // CM và AN = CM.
d) Chứng minh M, O và N thẳng hàng.
e) Đường chéo BD cắt AN ở I và CM ở Q. Chứng minh BQ = QI = ID.
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh A B 2 = B H . B C ; b) Chứng minh A H 2 = B H . C H ;
c) Gọi P là trung điểm của BH và Q là trung điểm của AH. Chứng minh Δ B A P ∽ Δ A C Q ;
d) Chứng minh A P ⊥ C Q .
Cho △ABC vuông tại A,kẻ đường cao AH
a) Chứng minh △ABC đồng dạnh với △HAC và AB.AC=AH.BC
b) Chứng minh AC2=HC.BC
c) Chứng minh AH2=HB.HC
a) Chứng minh rằng tứ giác 𝐵𝐻𝐶𝐷 là hình bình hành.
b) Biết 𝐵𝐴𝐶 ̂ = 60^𝑜, tính số đo góc 𝐵𝐻𝐶 ̂.
c) Chứng minh rằng 𝐻, 𝐸, 𝐷 thẳng hàng.
d) Chứng minh rằng 𝐴𝐻 = 2𝐹𝐸 và 𝐹𝐸 ⊥ 𝐵𝐶.
e) Chứng minh rằng 𝐴𝐻 = 2𝐼𝐽 và 𝐻, 𝐺, 𝐹 thẳng hàng
