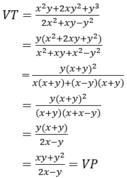Các câu hỏi tương tự
chứng minh các đẳng thức sau (x-y)^3 +4y(2x^2+y^2)=(x+y)^3+2y(x^2+y^2)
Chứng minh đẳng thức sau :
a) x^3 - y^3 + xy ( x-y ) = ( x-y ) ( x+ y ) ^2
b) x^3 + y ^3 - xy ( x+y ) = ( x+ y )( x-y ) ^2
chứng minh đẳng thức sau: (x+y)(x+y+z)-2(x-1)(y+1)+2=x^2+y^2
chứng minh đẳng thức (x-y)^3+4y(2x^2+y^2)=(x+y)^3+2y(x^2+y^2)
chứng minh đẳng thức sau: (x+y)(x+y+z)-2(x-1)(y+1)+2=x^2+y^2
Chứng minh các bất đẳng thức sau với x, y, z > 0
a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)
c) \(x^4+y^4\ge\dfrac{\left(x+y\right)^4}{8}\)
e) \(x^2+y^2+z^2\ge\dfrac{\left(x+y+z\right)^2}{3}\)
f) \(x^3+y^3+z^3\ge3xyz\)
Chứng minh các đẳng thức sau:
a) (x-1) (x^2 + x+ 1) = x^3 -1
b) (x^3+x^2y + xy^2 + y^3) (x-y) = x^4 - y^4
c) (x+y+z)^2 = x^2 + y^2 + z^2 + 2xy + 2 yz + 2zx
Chứng minh các đẳng thức sau: 2 ( x - y ) 3 ( y - x ) = - 2 3 ( v ớ i x ≠ y )
Chứng minh đẳng thức sau:
x^2n+1 + y^2n+1= (x+y)(x^2n - x^2n-1 y + x^2n-2 y^2-...+x^2 y^2n-2 -xy^2n-1 +y^2n)
chứng minh đẳng thức (x+y)(x+y+z)-2(x+1)(y+1)+2=x^2+y^2