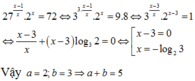Các câu hỏi tương tự
Phương trình 27 x - 1 x . 2 x = 72 có một nghiệm được viết dưới dạng x = - log a b với a,b là các số nguyên dương. Khi đó tổng a+b có giá trị bằng
A. 4
B. 5
C. 6
D. 8
Biết phương trình
27
x
-
1
x
.
2
x
27
có một nghiệm viết dưới dạng
x
-
log
a
b
, với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng
S
a
2
+
b...
Đọc tiếp
Biết phương trình 27 x - 1 x . 2 x = 27 có một nghiệm viết dưới dạng x = - log a b , với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng S = a 2 + b 2 .
A. S = 29
B. S = 25
C. S = 13
D. S = 34
Phương trình
2
x
-
2
3
x
2
+
2
x
-
8
có một nghiệm dạng
x
log
a
b
-
4
với a, b là các số nguyên dương thuộc khoảng (1;5) . Khi đó a+2b bằn...
Đọc tiếp
Phương trình 2 x - 2 = 3 x 2 + 2 x - 8 có một nghiệm dạng x = log a b - 4 với a, b là các số nguyên dương thuộc khoảng (1;5) . Khi đó a+2b bằng
A. 6
B. 14
C. 9
D. 7
Phương trình
log
2
x
-
x
2
-
1
log
3
x
+
x
2
-
1
log
6...
Đọc tiếp
Phương trình log 2 x - x 2 - 1 log 3 x + x 2 - 1 = log 6 x - x 2 - 1 có một nghiệm bằng 1 và một nghiệm còn lại dạng x = 1 2 a log b c + a - log b c , trong đó a, b, c là các số nguyên dương và a, c là các số nguyên tố và a > c. Giá trị biểu thức a 2 - 2 b + 3 c bằng
A. 0
B. 3.
C. 6.
D. 4.
Phương trình
5
x
2
-
3
x
+
2
3
x
-
2
có 1 nghiệm dạng
x
log
a
b
với a, b là các số nguyên dương lớn hơn 4 và nhỏ hơn 16. Khi đó a+2b bằng A. 35 B. 30 C....
Đọc tiếp
Phương trình 5 x 2 - 3 x + 2 = 3 x - 2 có 1 nghiệm dạng x = log a b với a, b là các số nguyên dương lớn hơn 4 và nhỏ hơn 16. Khi đó a+2b bằng
A. 35
B. 30
C. 40
D. 25
Phương trình
5
x
2
−
3
x
+
2
3
x
−
2
có 1 nghiệm dạng
x
log
a
b
với a, b là các số nguyên dương lớn hơn 4 và nhỏ hơn 16. Khi đó
a
+
2
b
bằng A. 35 ...
Đọc tiếp
Phương trình 5 x 2 − 3 x + 2 = 3 x − 2 có 1 nghiệm dạng x = log a b với a, b là các số nguyên dương lớn hơn 4 và nhỏ hơn 16. Khi đó a + 2 b bằng
A. 35
B. 30
C. 40
D. 25
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
f
x
x
-
6
x
2
+
4
trên đoạn [0;3] có dạng
a
-
b
c
với a là số nguyên và b, c là các số nguyên dương. Tính S a + b+ c A. S 4 B. S -2 C. S -22 D. S 5
Đọc tiếp
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x = x - 6 x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b+ c
A. S = 4
B. S = -2
C. S =-22
D. S = 5
Biết rằng tập nghiệm S của bất phương trình
log
-
x
2
+
100
x
-
2400
2
có dạng
S
a
;
b
x
∘
. Giá trị của
a
+...
Đọc tiếp
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Số thực m nhỏ nhất để phương trình
8
x
+
3
x
.
4
x
+
(
3
x
2
+
1
)
2
x
(
m
3
-
1
)
x
3
+
(
m
-
1
)
x...
Đọc tiếp
Số thực m nhỏ nhất để phương trình 8 x + 3 x . 4 x + ( 3 x 2 + 1 ) 2 x = ( m 3 - 1 ) x 3 + ( m - 1 ) x có nghiệm dương là a+e lnb, với a,b là các số nguyên. Giá trị của biểu thức a+b bằng
A. 7.
B. 4.
C. 5.
D. 3.