Ta có: A B → . C D → = A C → . B D → = A D → . C B → = 0
⇒ A B → ( A D → - A C → ) = A C → ( A D → - A B → ) = A D → ( A B → - A C → ) = 0
⇒ A B → . A C → = A C → . A D → = A B → . A D →
Đáp án C
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình tứ diện ABCD có AB=c, CD=c', AC=b, BD=b', BC=a, AD=a'. Tính góc giữa các vecto BC và DA
cho tứ diện ABCD và điểm M nằm trong tứ diện, qua M dựng các mặt phẳng (a) song song (BCD), (b) song song (ACD), (c) song song (ABD), (d) song song (ABC). Biết (a) cắt AB tại E, (b) cắt BC tại F, (c) cắt CD tại P, (d) cắt AD tại Q
cmr: \(\sqrt{\dfrac{EA}{EB}}+\sqrt{\dfrac{FB}{FC}}+\sqrt{\dfrac{PC}{PD}}+\sqrt{\dfrac{QD}{QA}}\ge4\sqrt{3}\)
Câu 25: Cho tứ diện
ABCD
và đặt
AB a AC b AD c = = =
, ,
. Gọi
M
là trung điểm của cạnh
CD
. Véc tơ
2BM
bằng:
A.
− + + 2a b c . B.
− + + 2abc . C. - − + + abc . D.
a b c − +
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, ABa, ACb, ADc Tính thể tích V của khối tứ diện ABCD theo a, b, c
Đọc tiếp
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
Cho tứ diện ABCD và đặt
A
B
→
a
→
,
A
C
→
b
→
v
à
A
D
→
c
→...
Đọc tiếp
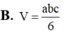
Cho tứ diện ABCD và đặt A B → = a → , A C → = b → v à A D → = c → . Gọi M là trung điểm của CD.
Vecto C D → bằng:
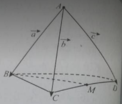
A. c → - b →
B. b → - c →
C. c → + b →
D. a → + b → + c →
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Điểm cách đều bốn điểm A, B, C, D là:
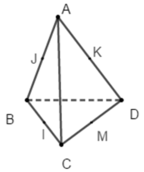
A. trung điểm J của AB
B. trung điểm I của BC
C. trung điểm K của AD
D. trung điểm M của CD
Cho
A
T
u
→
A
;
B
T
u
→
B
;
C
T
u
→
C
;
D
T
u
→
D
và AB BC + CD thì: A. AB BC – CD B. AC AB + DC’ C.BC BA +...
Đọc tiếp
Cho A ' = T u → A ; B ' = T u → B ; C ' = T u → C ; D ' = T u → D và AB = BC + CD thì:
A. A'B' = B'C' – C'D'
B. A'C' = A'B' + D'C’
C.B'C' = B'A' + A'C'
D. A'B' = B'C' + C'D'
Cho tứ diện ABCD và đặt
A
B
→
a
→
,
A
C
→
b
→
v
à
A
D
→
c
→...
Đọc tiếp
Cho tứ diện ABCD và đặt A B → = a → , A C → = b → v à A D → = c → . Gọi M là trung điểm của CD.
Vecto 2 B M → bằng:
A. - 2 a → + b → + c →
B. - a → + b → + c →
C. a → + b → + c →
D. a → - 2 b → + c →
cho hình chóp tứ giác S.ABCD có SB vuông góc BC và đáy ABCD là hình vuông, Xác định các cặp đường thẳng vuông góc sau
a) AB vuông góc D...?
AB vuông góc C...?
b) CD vuông góc B...?
CD vuông góc A...?
c) BC vuông góc S...?
AD vuông góc S...?
Cho tứ diện đều ABCD đều có cạnh bằng a
a) tính góc giữa hai đường thẳng AB và CD ,AD và BC
b) tính góc giữa các vectơ AC và AB ,AC VÀ DA
Xem chi tiết