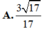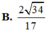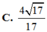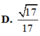Đáp án D
Phép tịnh tiến bảo toàn khoảng cách giữa 2 điểm
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Gọi A, B, C tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng:
A
B
→
.
A
C
→
k
2
.
A
B
→
....
Đọc tiếp
Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng: A ' B ' → . A ' C ' → = k 2 . A B → . A C →
Cho hình hộp ABCD A B C D . A'B C'D ' có :
AB=1, AD=2, A A'=3. Góc BAD =120 độ, BAA= 60 độ , DAA=60 độ . Gọi I là giao điểm của BC' và BC' . 1) Tính các tích sau AB .AD ,AB. AA' ,AD. AA'. 2) Tính AI AC . 3) Tính AI . 4) Tính góc giữa AI và AC'.Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, AA AB AC BC 2a (a0).
A
.
a
3
3
2
B
.
a
3
3
C
.
a
3
3...
Đọc tiếp
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, A'A = A'B = A'C = BC = 2a (a>0).
A . a 3 3 2
B . a 3 3
C . a 3 3 6
D . a 3 3 3
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác vuông tại A, AB a, AC
a
3
Hình chiếu vuông góc của A lên mặt phẳng (ABC) là trung điểm H của BC, HA
a
5
Gọi
φ
là góc giữa hai đường thẳng AB và BC. Tính cos
φ
A.cos
φ
7...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB = a, AC = a 3 Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm H của BC, HA' = a 5 Gọi φ là góc giữa hai đường thẳng A'B và B'C.
Tính cos φ
A.cos φ = 7 3 48
B. cos φ = 3 2
C. cos φ = 1 2
D. cos φ = 7 3 24
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, biết A'A=A'B=A'C=4a. Hình chóp A’.ABC có tất cả bao nhiêu mặt phẳng đối xứng?
A. 3.
B. Không có.
C. 4.
D. 2.
20 tháng 4 2023 lúc 9:09
Cho hình lăng trụ tam giác đều ABC.A'B'C' có \(AB=2\sqrt{3};AA'=2\)
Gọi M và N lần lượt là trung điểm của A'C' và A'B'. Tính \(cos\left(\widehat{\left(AB'C'\right);\left(BCMN\right)}\right)\)
Cho hình lăng trụ ABC.A'B'C'. Gọi H là trung điểm của A'B'. Đường thẳng B'C song song với mặt phẳng nào sau đây?
A. (AHC')
B. (AA'H)
C. (HAB)
D. (HA'C')
Cho hình lập phương ABCD.ABCD có khoảng cách giữa AC và CD là 1 cm. Thể tích khối lập phương ABCD.ABCD là: A. 8
c
m
3
. B.
2
2
c
m
3
. C.
3...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có khoảng cách giữa A'C và C'D' là 1 cm. Thể tích khối lập phương ABCD.A'B'C'D' là:
A. 8 c m 3 .
B. 2 2 c m 3 .
C. 3 3 c m 3 .
D. 27 c m 3
Trong mặt phẳng (α) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong (α). Trên Ax lấy đoạn AA a, trên By lấy đoạn BB b, trên Cz lấy đoạn CC c.a) Gọi I, J và K lần lượt là các giao điểm BC, CA và AB với (α).Chứng minh rằng
I
B
I
C
.
J
C
J...
Đọc tiếp
Trong mặt phẳng (α) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong (α). Trên Ax lấy đoạn AA' = a, trên By lấy đoạn BB' = b, trên Cz lấy đoạn CC' = c.
a) Gọi I, J và K lần lượt là các giao điểm B'C', C'A' và A'B' với (α).
Chứng minh rằng I B I C . J C J A . K A K B = 1
b) Gọi G và G' lần lượt là trọng tâm của các tam giác ABC và A'B'C'.
Chứng minh: GG′ // AA′.
c) Tính GG' theo a, b, c
Cho hình lập phương ABCD.ABCD Gọi E. F lần lượt là trung điểm các cạnh BC, CD Côsin góc giữa hai mặt phẳng (AEF) và (ABCD) bằng
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D Gọi E. F lần lượt là trung điểm các cạnh B'C', C'D' Côsin góc giữa hai mặt phẳng (AEF) và (ABCD) bằng
