Các câu hỏi tương tự
Cho tứ diện ABCD và đặt
A
B
→
a
→
,
A
C
→
b
→
v
à
A
D
→
c
→...
Đọc tiếp
Cho tứ diện ABCD và đặt A B → = a → , A C → = b → v à A D → = c → . Gọi M là trung điểm của CD.
Vecto C D → bằng:
A. c → - b →
B. b → - c →
C. c → + b →
D. a → + b → + c →
Câu 25: Cho tứ diện
ABCD
và đặt
AB a AC b AD c = = =
, ,
. Gọi
M
là trung điểm của cạnh
CD
. Véc tơ
2BM
bằng:
A.
− + + 2a b c . B.
− + + 2abc . C. - − + + abc . D.
a b c − +
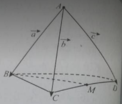
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
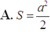


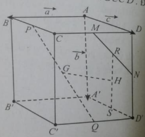
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Vecto M N → bằng:
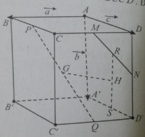
A. 1 2 c → - a →
B. 1 2 c → - b →
C. 1 2 b → - a →
D. 1 2 a → - b →
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
c) Chứng minh GA = 3GA’
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt
A
B
→
b
→
;
A
C
→
c
→
;
A
D
→...
Đọc tiếp
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d . Khẳng định nào sau đây đúng?
![]()
![]()
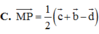
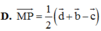
Cho hình chóp SABCD đáy ABCD là hình vuông cạnh bên bằng 6cm tâm O gọi e,f lần lượt là trung điểm của SA,SD a) tìm giao điểm I của (OEF) b) Gọi K là giao điểm của (SBI) với AD C/m: B,I,K thẳng hàng C) tìm thiết diện của (OEF) với h/chóp D) tính diện tích thiết diện đó biết FH vuông góc OI tại trung điểm H của OI
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC. Gọi I là giao điểm của đường thẳng AM với mặt phẳng (SBD). Khi đó tỉ số \(\dfrac{MA}{IA}\) bằng bao nhiêu?
A. \(\dfrac{4}{3}\)
B. 3
C. 2
D. \(\dfrac{3}{2}\)
Bt2: cho hình chóp S.ABCD đáy là tứ giác lồi có AB>CD .gọi M,N lần lượt là trung điểm của cạnh SA và SD .a) tìm giao tuyến (SAB) và (SCD).b) tìm giao tuyến của (MNC) và (ABCD).c)tìm giao điểm của MN và (ABN).d) tìm thiết diện của hình chóp vs mp (BMN)