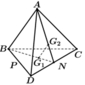
Gọi N là trung điểm của CD
● Khi đó A, G 2 , N thẳng hàng và B, G 1 , N thẳng hàng.
Do đó, B G 1 , A G 2 và CD đồng quy
Áp dụng định lí Talet đảo, suy ra
Do đó D sai. Chọn D.
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và tam giác ABC. Mệnh đề nào dưới đây đúng?
A. GE cắt CD.
B. GE cắt AD.
C. GE, CD chéo nhau.
D. GE // CD
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây là đúng?
A. GE và CD chéo nhau
B. GE//CD
C. GE cắt AD
D. GE cắt CD
Cho tứ diện ABCD Gọi G,E lần lượt là trọng tâm của tam giác A B D v à A B C . Mệnh đề nào dưới đây đúng:
A. G E v à CD chéo nhau
B. G E / / C D
C. GE và AD
D. GE cắt CD
Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi G 1 là giao điểm của AG và mp(BCD), G 2 là giao điểm của BG và mp(ACD). Khẳng định nào sau đây là đúng?
A. G 1 G 2 / / A B
B. G 1 G 2 / / A C
C. G 1 G 2 / / C D
D. G 1 G 2 / / A D
Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mặt phẳng (ACD) là
A. điểm F
B. giao điểm của đường thẳng EG và AC
C. giao điểm của đường thẳng EG và CD
D. giao điểm của đường thẳng EG và AF
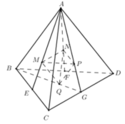
Cho khối tứ diện ABCD có thể tích là V. Gọi E, F, G lần lượt là trung điểm BC, BD, CD và M, N, P, Q lần lượt là trọng tâm ∆ A B C ; ∆ A B D ; ∆ A C D ; ∆ B C D . Tính thể tích khối tứ diện MNPQ theo V.
A. V 9
B. V 3
C. 2 V 9
D. V 27
Cho tứ diện đều ABCD. Gọi G là trọng tâm tam giác ABC. Chọn khẳng định đúng trong các khẳng định sau:
A. BG ⊥ ACD
B. DG ⊥ ACB
C. DA ⊥ ABC
D. AG ⊥ BCD
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AD, BC; G là trọng tâm của tam giác BCD. Khi đó, giao điểm của đường thẳng MG và mp (ABC) là:
A. Giao điểm của đường thẳng MG và đường thẳng AN
B. Điểm N
C. Giao điểm của đường thẳng MG và đường thẳng BC
D. Điểm A
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm đối xứng của G mặt phẳng (ABC). Thể tích khối đa diện SABCD là:
A. a 3 2
B. a 3 2 3
C. a 3 2 6
D. a 3 2 9
