Các câu hỏi tương tự
Cho tứ diện ABCD có
A
B
C
D
a
,
A
C
B
D
b
,
A
D
B
C
c
. Gọi
α
là số đo của góc hợp bởi hai đường thẳng AB, CD. Khi đó
cos
α
bằng A.
b
2
-...
Đọc tiếp
Cho tứ diện ABCD có A B = C D = a , A C = B D = b , A D = B C = c . Gọi α là số đo của góc hợp bởi hai đường thẳng AB, CD. Khi đó cos α bằng
A. b 2 - c 2 a 2
B. b 2 - c 2 2 a 2
C. a 2 2 b 2 + c 2
D. a 2 b 2 + c 2
Cho tứ diện ABCD có AB CD a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng
30
°
. A.
M
N
a
2
B.
M
N
a
3
2
C.
M
N
a
3...
Đọc tiếp
Cho tứ diện ABCD có AB = CD = a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30 ° .
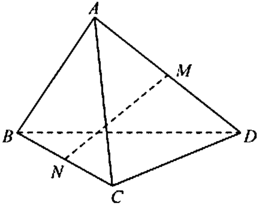
A. M N = a 2
B. M N = a 3 2
C. M N = a 3 3
D. M N = a 4
Cho tứ diện ABCD có
A
B
C
D
a
. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng
30
°
.
A.
M
N
a
2
B.
M
N
a
3
2
C.
M...
Đọc tiếp
Cho tứ diện ABCD có A B = C D = a . Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30 ° .
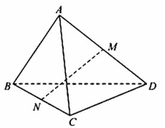
A. M N = a 2
B. M N = a 3 2
C. M N = a 3 3
D. M N = a 4
Cho tứ diện đều ABCD, gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi là số đo của góc giữa hai đường thẳng AN, CM. Khi đó cosα bằng
A. 2 3
B. 1 3
C. 1
D. 2
Cho tứ diện ABCD có
A
B
C
D
2
a
. Gọi M, N lần lượt là trung điểm của BC, AD và
M
N
a
3
. Tính góc tạo bởi hai đường thẳng AB và CD A.
30
°
B.
45
°
C.
60
°
D.
90
°
Đọc tiếp
Cho tứ diện ABCD có A B = C D = 2 a . Gọi M, N lần lượt là trung điểm của BC, AD và M N = a 3 . Tính góc tạo bởi hai đường thẳng AB và CD
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Cho tứ diện ABCD có BD vuông góc với AB và CD. Gọi P và Q lần lượt là trung điểm của của các cạnh CD và AB thỏa mãn BD:CD:PQ:AB = 3:4:5:6 . Gọi φ là góc giữa hai đường thẳng AB và CD. Giá trị của cosφ bằng
A. 7/8.
B. 1/2.
C. 11/16.
D. 1/4.
Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của BC và AD. Biết
A
B
C
D
a
,
M
N
a
3
2
. Tính góc giữa hai đường thẳng AB và CD. A.
45
°
B.
30
°
C.
60
°
D.
90
°
Đọc tiếp
Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của BC và AD.
Biết A B = C D = a , M N = a 3 2 . Tính góc giữa hai đường thẳng AB và CD.
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T) A.
S
a
2
2
B.
S
a
2
3
6
C. ...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
A. S = a 2 2
B. S = a 2 3 6
C. S = a 2 3 9
D. S = a 2 6
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T). A.
S
a
2
2
.
B.
S
a
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T).
A. S = a 2 2 .
B. S = a 2 3 6 .
C. S = a 2 3 9 .
D. S = a 2 6 .




