Question

Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.

Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.

Answer 1

Vì tam giác ABC là tam giác đều nên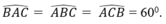 

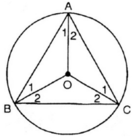
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC

* Xét tam giác AOB có:

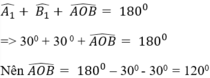
* Tượng tự ta được: 

Answer 2

a) Ta có : ^A = ^B = ^C =60^o ( gt )

Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC

Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o

=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o

Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o

b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :

\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)

\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)