Do ![]()
nên số đo các cung nhỏ AB,BC và AC là:![]()
Suy ra,số đo các cung lớn AB, AC và BC là: 3600 - 1200 = 2400

Do ![]()
nên số đo các cung nhỏ AB,BC và AC là:![]()
Suy ra,số đo các cung lớn AB, AC và BC là: 3600 - 1200 = 2400
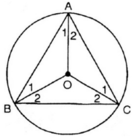
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
Cho ba đường tròn O1 ; O2 ; O3 cùng bán kính và cùng đi qua một điểm I , Gọi các giao điểm của hai trong ba đường tròn khác I lần lượt là A ; B ; C . CMR
a) TAm giác ABC = tam giác O1O2O3
b) I là trực tâm tam giác ABC
Bài 1: Cho nửa đường tròn (O) đường kính AB. Lấy điểm C trên đoạn AO, C khác A và O. Đường thẳng đi qua C vuông góc với AO cắt nửa đường tròn (O) tại D. M là điểm bất kì trên cung BD ( M khác B và D). Tiếp tuyến tại M của (O) cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và CD.
a/ CM bốn điểm B,C,F,M cùng nằm trên một đường tròn.
b/ CM: EM = EF
c/ Gọi I là tâm đường tròn ngoại tiếp tam giác DMF. CM góc ABI có số đo không đổi khi M di động trên cung \(\widebat{BD}\)
Bài 2: Cho tam giác đều ABC nội tiếp trong đường tròn (O). Một đường thẳng d thay đổi đi qua A, cắt (O) tại điểm thứ hai là E, cắt hai tiêp tuyến kẻ từ B và C của đường tròn (O) lần lượt tại M và N sao cho A,M,N nằm ở cùng nửa mặt phẳng bờ BC. Gọi giao điểm của hai đường thẳng MC và BN tại F. CMR:
a/ Hai tam giác MBA và CAN dồng dạng và tích MB.CN không đổi.
b/ Tứ giác BMEF nội tiếp trong một đường tròn.
c/ Đường thẳng EF luôn đi qua một điểm cố định khi (d) thay đổi.
Cho đường tròn(O;R) và dây BC cố định ko đi qua tâm O.Lấy điểm A bất kì trên cung lớn BC khác B,C . Ba đường cao AD,BE,CF của tam giác ABC cắt nhau tại điểm H.
a) Chứng minh các tứ giác HDBF,BCEF nội tiếp đường tròn
b) Chứng minh DA là phân giác của góc EDF
c) Gọi K là điểm đối xứng của A qua tâm O.Chứng minh HK đi qua trung điểm của đoạn BC
d)Giả sử góc BAC=60o .Chứng minh AHO là tam giác cân
Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tròn tâm D bán kính R, cung này cắt (O) ở B và C
a, Tứ giác OBDC là hình gì? Vì sao?
b, Tính số đo các góc C B D ^ ; C B O ^ ; O B A ^
c, Chứng minh tam giác ABC là tam giác đều
Cho đường tròn (O). Đường thẳng (d) không đi qua tâm (O) cắt đường tròn tại hai điểm A và B theo thứ tự, C là điểm thuộc (d) ở ngoài đường tròn (O). Vẽ đường kính PQ vuông góc với dây AB tại D ( P thuộc cung lớn AB), Tia CP cắt đường tròn (O) tại điểm thứ hai là I, AB cắt IQ tại K.
a. Chứng minh tứ giác PDKI nội tiếp đường tròn.
b. Chứng minh CI.CP = CK.CD
c. Chứng minh IC là phân giác của góc ngoài ở đỉnh I của tam giác AIB.
d. Cho ba điểm A, B, C cố định. Đường tròn (O) thay đổi nhưng vẫn đi qua A và B. Chứng minh rằng IQ luôn đi qua một điểm cố định.
Cho đường tròn (O). Đường thẳng (d) không đi qua tâm (O) cắt đường tròn tại hai điểm A và B theo thứ tự, C là điểm thuộc (d) ở ngoài đường tròn (O). Vẽ đường kính PQ vuông góc với dây AB tại D ( P thuộc cung lớn AB), Tia CP cắt đường tròn (O) tại điểm thứ hai là I, AB cắt IQ tại K.
a. Chứng minh tứ giác PDKI nội tiếp đường tròn.
b. Chứng minh CI.CP = CK.CD
c. Chứng minh IC là phân giác của góc ngoài ở đỉnh I của tam giác AIB.
d. Cho ba điểm A, B, C cố định. Đường tròn (O) thay đổi nhưng vẫn đi qua A và B. Chứng minh rằng IQ luôn đi qua một điểm cố định.
Cho tam giác ABC có số đo góc
ABC = 40
, số đo góc
ACB = 30
. Vẽ đường tròn tâm B bán kính BA
và đường tròn tâm C bán kính CA, chúng cắt nhau tại điểm thứ hai là D (khác A). Lấy điểm M trên cung lớn
AD của đường tròn tâm B (M khác A và D), các tia MA, MD cắt đường tròn tâm C tại điểm thứ hai lần lượt tại
N và P (khác A và D). Số đo của cung nhỏ NP bằng:
cho tam giác nhọn ABC nội tiếp đường tròn tâm O. M là điểm chính giữa cung BC không chứa điểm A. Gọi M' là điểm đối xứng với M qua O. Các đường phân giác trong góc B và góc C của tam giác ABC cắt đường thẳng AM' lần lượt tại E và F.
1/Chứng minh tứ giác BCEF nội tiếp được trong đường tròn
2/Biết đường tròn nội tiếp tam giác ABC có tâm I bán Kính r.
Chứng Minh: IB.IC = 2r.IM