Các câu hỏi tương tự
Cho tam giác ABC vuông tại A. Kẻ đường cao AH, gọi M là một điểm trên cạnh BC, kẻ MI vuông góc với AB tại I, MK vuông góc với AC tại K. Chứng minh rằng: góc IHK = 90 độ
Cho tam giác ABC vuông tại A (AB>AC) có AH là đường cao. Kẻ HM vuông góc AB tại M, kẻ HN vuông góc AC tại N.
a) Chứng minh: tứ giác AMHN là hình chữ nhật.
b) Gọi K là chung điểm của BC, qua K kẻ đường vuông góc với BC cắt AC tại E. Gọi F là điểm đối xứng với E qua K. Chứng minh: tứ giác BECF là hình thoi.
Cho tam giác ABC nhọn có AB AC, đường cao BH. Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D vả kẻ MK vuông góc với AB tại K. Gọi E là điểm đối xứng với K qua đường thẳng BCa, C m rằng góc BMK Cho tam giác ABC nhọn có AB AC, đường cao BH.Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D và kẻ MK vuông góc với AB tại K. Gọi E là điểm điểm đối xứng với k qua đường thẳng BC.a, C m rằng góc BMK góc CMDTừ đó c m 3 điểm E,M,D thẳng hàngb,Tứ giác BEDH là hình gì Tại sao c, So s...
Đọc tiếp
Cho tam giác ABC nhọn có AB AC, đường cao BH. Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D vả kẻ MK vuông góc với AB tại K. Gọi E là điểm đối xứng với K qua đường thẳng BCa, C m rằng góc BMK Cho tam giác ABC nhọn có AB AC, đường cao BH.Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D và kẻ MK vuông góc với AB tại K. Gọi E là điểm điểm đối xứng với k qua đường thẳng BC.a, C m rằng góc BMK góc CMDTừ đó c m 3 điểm E,M,D thẳng hàngb,Tứ giác BEDH là hình gì Tại sao c, So sánh MK MD và BHd, Cho BH= 8cm, CH= 6cm, AC= 12cmTính chiều cao của tam giác ABC được kẻ từ đỉnh A.
Cho tam giác ABC nhọn có AB AC, đường cao BH. Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D vả kẻ MK vuông góc với AB tại K. Gọi E là điểm đối xứng với K qua đường thẳng BCa, C m rằng góc BMK Cho tam giác ABC nhọn có AB AC, đường cao BH.Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D và kẻ MK vuông góc với AB tại K. Gọi E là điểm điểm đối xứng với k qua đường thẳng BC.a, C m rằng góc BMK góc CMDTừ đó c m 3 điểm E,M,D thẳng hàngb,Tứ giác BEDH là hình gì Tại sao c, So s...
Đọc tiếp
Cho tam giác ABC nhọn có AB AC, đường cao BH. Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D vả kẻ MK vuông góc với AB tại K. Gọi E là điểm đối xứng với K qua đường thẳng BCa, C m rằng góc BMK Cho tam giác ABC nhọn có AB AC, đường cao BH.Từ điểm M trên BC M khác B và C kẻ MD vuông góc với AC tại D và kẻ MK vuông góc với AB tại K. Gọi E là điểm điểm đối xứng với k qua đường thẳng BC.a, C m rằng góc BMK góc CMDTừ đó c m 3 điểm E,M,D thẳng hàngb,Tứ giác BEDH là hình gì Tại sao c, So sánh MK MD và BHd, Cho BH 8cm, CH 6cm, AC 12cmTính chiều cao của tam giác ABC được kẻ từ đỉnh A.
Cho tam giác ABC vuông tại A , có AB=4cm AC = 6cm kẻ đường cao AH từ H kẻ HE vuông góc với AB tại E từ H kẻ HK vuông góc với AC tại F. Gọi I và K lần lượt là trung điểm của HB và HC lấy điểm M trên đoạn FC sao ch FA=FM
a, chứng minh rằng AH=EF
b, Tứ giác EHMF là hình gì vì sao
c Tính DIỆN TÍCH TỨ GIÁC EIKF
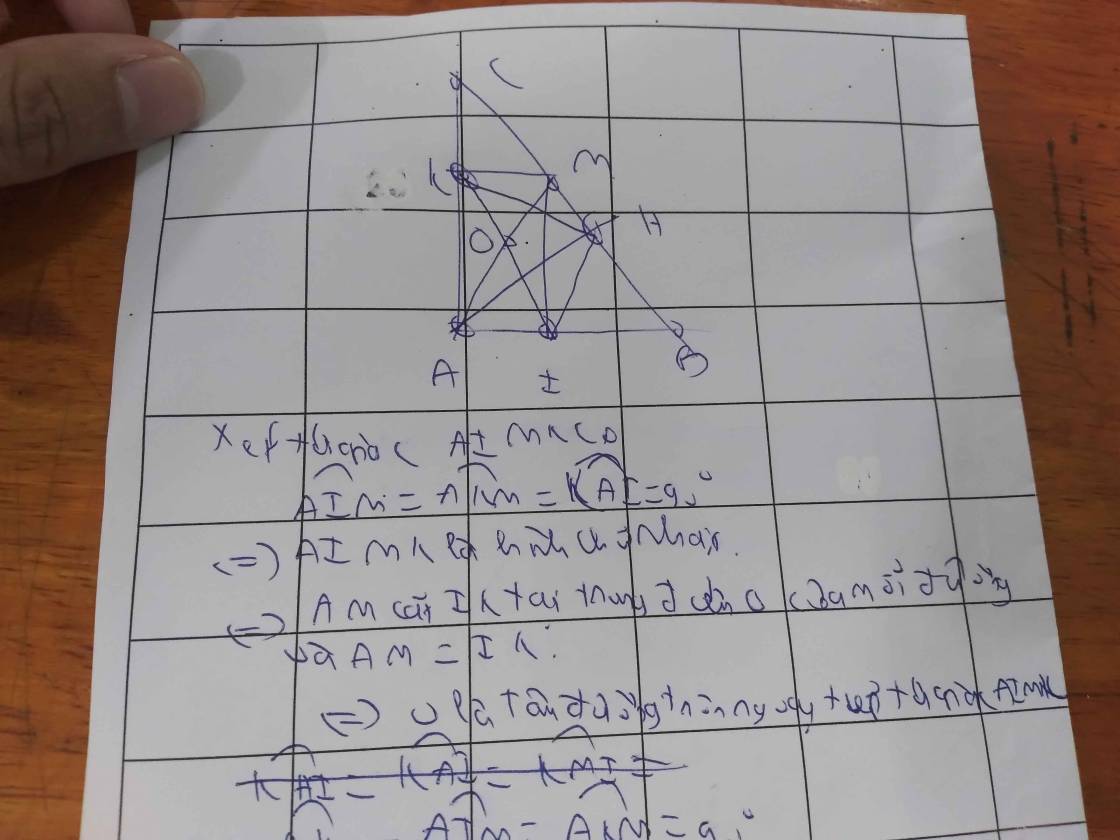
Cho tam giác ABC vuông cân tại A, có AH là đường cao. Gọi M là một điểm bất kì trên cạnh BC, I và K lần lượt là hình chiếu vuông góc của M trên AB, AC. Chứng minh tam giác IHK vuông cân.
Cho tam giác ABC vuông cân tại A , đường cao AH . Gọi M là một điểm bất kì trên cạnh BC . I , K lần lượt là hình chiếu vuông góc của M trên AB, AC . Chứng minh : Tam giác IHK vuông cân
Cho tam giác ABC vuông tại A (AB<AC). Lấy M,E lần lượt là trung điểm cạnh BC, kẻ MD vuông góc với AB tại D, kẻ ME vuông góc với AC tại E.
a) Chứng minh ADME là hình chữ nhật
b) Chứng minh DBME là hình bình hành
c) Kẻ đường cao AH của tam giác ABC. Chứng minh DEMH là hình thang cân
Cho tam giác ABC vuông tại A (AC > AB) đường cao AH (H ∈ BC).Trên tia đối của tia HB lấy điểm D sao cho HB = HD. Kẻ DE vuông góc với AC tại E và HK vuông góc với AC tại K. Gọi M là trung điểm của DC. Chứng minh góc HEM vuông