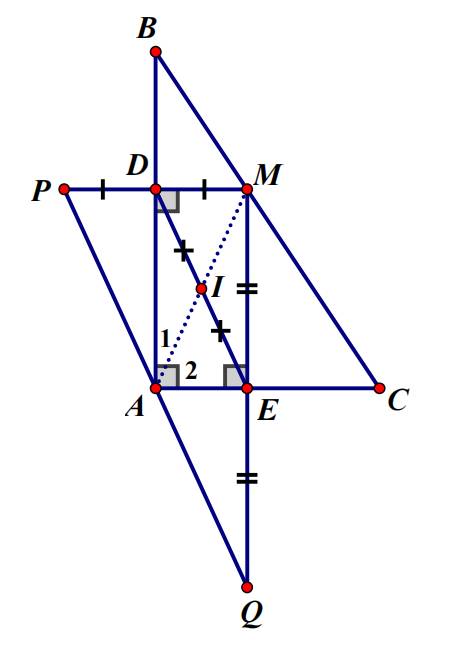
Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Kẻ DE vuông góc với AB tại E; DE vuông góc với AC tại F
a. Tứ giác AEDF là hình gì? Vì sao?
b. Trên tia DE lấy điểm M sao cho ME= DE. Chứng minh tứ giác ADBM là hình thoi
c. Trên tia đối của tia FD lấy điểm N sao cho FN= FD. Chứng minh A là trung điểm của đoạn thẳng MN
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó; E là trung điểm của AB
Xét ΔBAC có
D là trung điểm của BC
DF//AB
Do đó: F là trung điểm của AC
Xét tứ giác ADBM có
E là trung điểm chung của AB và DM
=>ADBM là hình bình hành
c: Xét tứ giác ADCN có
F là trung điểm chung của AC và DN
=>ADCN là hình bình hành
=>AN//CD và AN=CD
Ta có: ADBM là hình bình hành
=>AM//BD và AM=BD
Ta có: AN//CD
AM//BD
mà B,D,C thẳng hàng
nên AN//BC và AM//BC
mà AN,AM có điểm chung là A
nên N,A,M thẳng hàng
Ta có: AM=BD
AN=CD
mà BD=DC
nên AM=AN
mà M,A,N thẳng hàng
nên A là trung điểm của MN