Question

cho tam giác ABC vuông tại A có AB lớn hơn AC,BD là đường phân giác .DM vuông góc BC tại M.

a,chứng minh:tam giác DAB=tam giác DMB

b,BD là đường trung trực của AM

c,tam giác BAM,tam giác DAM là tam giác gì?vì sao?

d,so sánh AD và AC

Answer 1

  

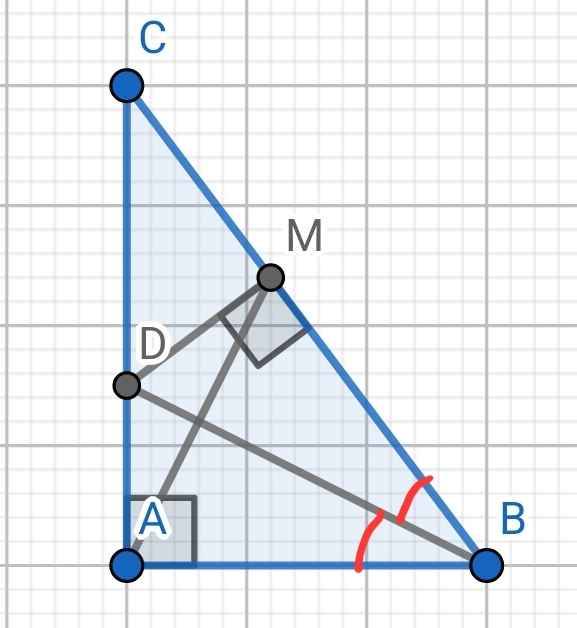
a) Xét hai tam giác vuông: ∆DAB và ∆DMB có:

DB chung

∠ABD = ∠MBD (do BD là tia phân giác của ∠B)

⇒ ∆DAB = ∆DMB (cạnh huyền - góc nhọn)

b) Do ∆DAB = ∆DMB (cmt)

⇒ DA = DM (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AM (1)

Do ∆DAB = ∆DMB (cmt)

⇒ BA = BM (hai cạnh tương ứng)

⇒ B nằm trên đường trung trực của AM (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AM

c) ∆BAM có BA = BM (cmt)

⇒ ∆BAM cân tại B

∆DAM có DA = DM (cmt)

⇒ ∆DAM cân tại D

d) Do D ∈ AC

⇒ AD < AC