Question

Cho tam giác ABC vuông tại A (AB<AC),có đường trung tuyến AI.Kẻ IM vuông góc với AB tại M,và IN vuông góc với AC tại N.

a)C/m:AMIN là hình chữ nhật.

b)C/m:BM=IN và BMNI là hình bình hành.

Answer 1

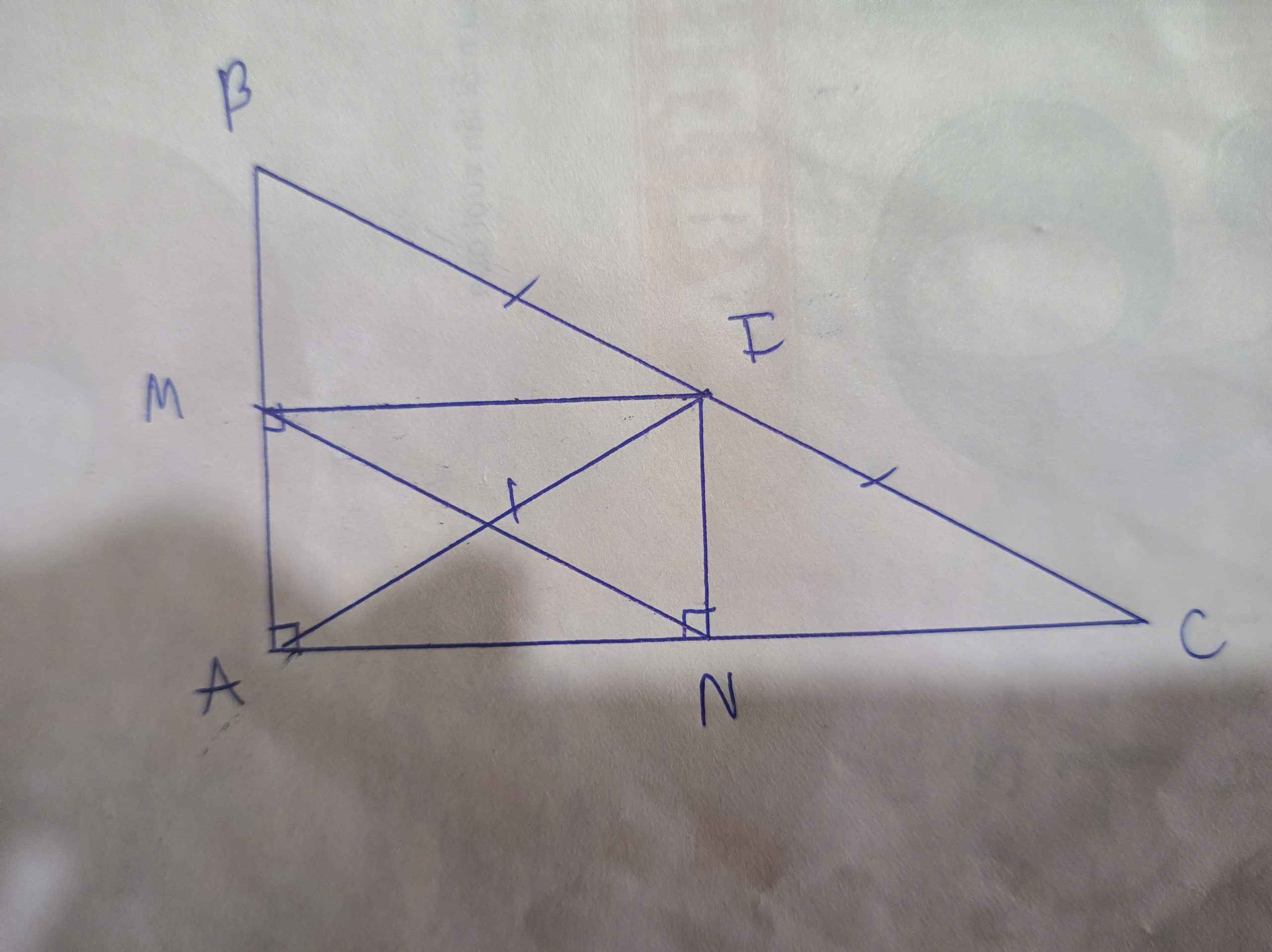
a: Xét tứ giác AMIN có \(\widehat{AMI}=\widehat{ANI}=\widehat{MAN}=90^0\)

nên AMIN là hình chữ nhật

b: Ta có: AMIN là hình chữ nhật

=>IM=AN và IN=AM

Xét ΔABC có 

I là trung điểm của BC

IN//AB

Do đó: N là trung điểm của AC

=>AN=NC

mà AN=IM

nên IM=NC

Xét ΔABC có

I là trung điểm của BC

IM//AC

Do đó: M là trung điểm của AB

=>MA=MB

mà MA=NI

nên MB=NI

Xét tứ giác BMNI có

BM//NI

BM=NI

Do đó: BMNI là hình binh hành

Answer 2

a. xét tứ giác AMIN có:

\(\widehat{IMA}=\widehat{MAN}=\widehat{ANI}=90^0\)

=> tứ giác AMIN là hình chữ nhật

b. xét tam giác ABI có IA = IB (vì tam giác ABC vuông tại A có AI là đường trung tuyến)

=> tam giác ABI là tam giác cân (tại I)

ta có IM là đường cao suy ra IM cũng là đường trung tuyến

=> MB = MA (1)

trong HCN AMIN có IN = MA (2)

từ (1) (2) => BM = IN (3)

ta có AB ⊥ AC và IN ⊥ AC

=> AB // IN hay BM // IN (4)

từ (3) và (4) => tứ giác BMIN là hình bình hành