Đáp án A
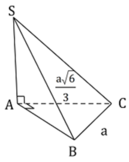
Em có: SA ⊥ ABC tại A
=> A là hình chiếu vuông góc của S trên (ABC)
=> AB là hình chiếu vuông góc của SB trên (ABC)

Đáp án A

Em có: SA ⊥ ABC tại A
=> A là hình chiếu vuông góc của S trên (ABC)
=> AB là hình chiếu vuông góc của SB trên (ABC)

Cho tam giác ABC có BC = a, B A C ⏜ = 135 ° . Trên đường thẳng vuông góc với (ABC) tại A lấy điểm S thỏa mãn SA = a 2 . Hình chiếu vuông góc của A trên SB , SC lần lượt là M , N . Góc giữa hai mặt phẳng (ABC) và (AMN) là?
A. 30 °
B. 45 °
C. 60 °
D. 75 °
Cho tam giác ABC có BC = a, BAC ^ = 135 o . Trên đường thẳng vuông góc với (ABC) tại A lấy S thỏa mãn SA = a 2 . Hình chiếu vuông góc của A trên SB, SC lần lượt là M, N. Góc giữa hai mặt phẳng (ABC) và (AMN) là
A. 30 o
B. 45 o
C. 60 o
D. 75 o
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , A B a , S A = S B = S C . Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45 ° Tính khoảng cách từ điểm S đến mặt phẳng (ABC)
A. a 3 3
B. a 2 2
C. a 2
D. a 3
Cho hình chóp S ABC . có tam giác SAB vuông cân tại S; tam giác ABC vuông cân tại C và ∠ B S C = 60 ° . Gọi M là trung điểm cạnh SB. Côsin góc giữa hai đường thẳng AB và CM bằng
A. 6 6
B. 30 6
C. 6 3
D. 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC = 2a, BC = a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 ° . Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A. a 39 13
B. 3 a 13 13
C. a 39 26
D. a 13 26
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, A B = a , S A = S B = S C . Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45 0 . Tính khoảng cách từ điểm S đến mặt phẳng (ABC)
A. a 3 3
B. a 2 2
C. a 2
D. a 3
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 45 0 .
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và A B C ^ = 60 ° . Hình chiếu vuông góc của điểm S lên mặt phẳng A B C D trùng với trọng tâm tam giác ABC. Gọi φ là góc giữa đường thẳng SB với mặt phẳng S C D , tính sin φ biết rằng S B = a .
A. sin φ = 2 2
B. sin φ = 2 3
C. sin φ = 3 2
D. sin φ = 6 2
Cho khối chóp S . A B C có đáy là tam giác vuông tại A, S B ⊥ A B C , A B = a , A C B ^ = 30 ° , góc giữa đường thẳng SC và mặt phẳng (ABC) là 60 ° . Tính thể tích V của khối chóp theo a.
A. V = 3 a 3
B. V = a 3
C. V = 2 a 3
D. V = 3 a 3 2