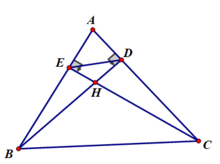
b) Xét tứ giác BDEC có:
∠(BEC) = ∠(BDC) = 90 0
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BDEC là tứ giác nội tiếp

b) Xét tứ giác BDEC có:
∠(BEC) = ∠(BDC) = 90 0
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BDEC là tứ giác nội tiếp
Cho tam giác abc có các góc nhọn nội tiếp đường tròn (o). Hai đường cao Bd và CE cắt nhau tại H. a) Chứng minh: Các tứ giác ADHE, BEDC nội tiếp. b) Chứng minh: Góc EAH = Góc ECB c) Từ A kẻ tiếp tuyến xy với đường tròn. Chứng minh: xy//DE
Cho tam giác ABC nhọn nội tiếp đường tròn (O).
Các đường cao BD, CE của tam giác ABC cắt nhau tại H
và cắt đường tròn (O) lần lượt tại M và N. Chứng minh:
a. Các tứ giác ADHE, BEDC nội tiếp
b. DE/MN
c. OA.LDE
1.Cho tam giác ABC nhọn. Kẻ các đường cao BD, CE cắt nhau tại H. Chứng mình rằng: a,AEHD là tứ giác nội tiếp b,BEDC là tứ giác nội tiếp. Tìm tâm đường tròn ngoại tiếp c, Góc EBD=ECD d,AH vuông góc với BC
2.Cho tam giác ABC có 3 góc nhọn. Các đường cao BM và CN cát nhau tại I. Chứng minh rằng: a,AMIN là một tứ giác nội tiếp b, Góc NAI=NMI c,AI cắt BC tại H. Chứng minh HA là tia phân giác của góc NHM
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O) Hai đường cao BD và CE cắt nhau tại H.Chứng minh rằng:
a.Tứ giác BEDC,AEHD là tứ giác nội tiếp;
b.DEC=DBC
c.Qua A vẽ tiếp tuyến xy của (O) chứng minh OA vuông góc với DE
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O . Hai đường cao BD và CE của tam giác ABC cắt nhau tại H, đường thẳng BD cắt đường tròn (O) tại điểm thứ hai P , đường thẳng CE cắt đường tròn (O) tại điểm thứ hai Q. Chứng minh rằng:
1) BEDC là tứ giác nội tiếp,
b) HQ.HC = HP.HB
3) DE // PQ
Cho tam giác ABC nhọn nội tiếp (O; R). Hai đường cao CE, BD lần lượt cắt đường tròn lần lượt tại E’, D’. Gọi H là trực tâm của tam ABC.
a/ Chứng minh: tứ giác AEHD, BEDC nội tiếp được
b/ Chứng minh: ED//E’D’ và OA vuông góc với ED
c/ Kẻ đường kính AA’. Gọi I là trung điểm của BC. C/m: Tứ giác HCA’B là hình bình hành, từ đó suy ra H, I, A’ thẳng hàng.
d/ Cho BC cố định, khi điểm A chuyển động trên cung lớn BC thì điểm H chuyển động trên đường nào.
Phần tự luận
Nội dung câu hỏi 1
Cho tam giác ABC nhọn, đường cao BD và CE cắt nhau tại H. Chứng minh rằng:
a) Tứ giác ADHE nội tiếp
Giải cho em bài này với ạ !
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O). Hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh tứ giác AEHD nội tiếp.
b) Chứng minh tứ giác BEDC nội tiếp được trong 1 đường tròn, xác định tâm I của đường tròn đó.
c) Chứng minh HE.HC = HB.HD
d) Chứng minh OA vuông góc với ED.
Cho tam giác ABC nhọn nối tiếp đường tròn (O) các đường cao BD và CE của tam giác ABC cắt nhau tại H chứng minh a) tứ giác AEHD nội tiếp đuong tròn b) cung AED_|_ACB c) OA_|_ED giúp tui zới