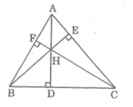
hình trang 121 sgbt)
Xét ∆ AFH và ∆ CDH, ta có:
ˆAFH=ˆCDH=90∘AFH^=CDH^=90∘
ˆAHF=ˆCHDAHF^=CHD^ (đối đỉnh)
Quảng cáo
Suy ra: ∆ AFH đồng dạng ∆ CDH (g.g)
Suy ra: AHCH=FHDHAHCH=FHDH
Suy ra: AH.DH = CH.FH (1)
Xét ∆ AEH và ∆ BDH, ta có:
ˆAEH=ˆBDH=90∘AEH^=BDH^=90∘
ˆAHE=ˆBHDAHE^=BHD^ (đối đỉnh)
Suy ra: ∆ AEH đồng dạng ∆ BDH (g.g)
Suy ra: AHBH=EHDHAHBH=EHDH
Suy ra: AH.DH = BH.EH (2)
Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.
#HT#
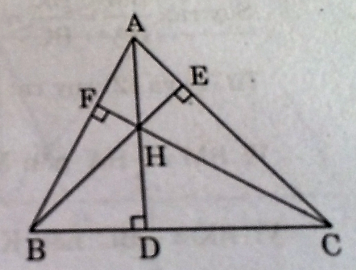
Xét \(\Delta\)AFH và \(\Delta\)CDH có:
\(\widehat{AFH}\)= \(\widehat{CDH}\)(=90)
\(\widehat{AHF}\)= \(\widehat{CHD}\)( đối đỉnh)
=> \(\Delta\)AFH đồng dạng \(\Delta\)CDH
=> \(\frac{AH}{CH}=\frac{FH}{DH}\)
=>AH . DH = CH .FH(1)
Xét \(\Delta\)AEH và \(\Delta\)BDH,ta có:
\(\widehat{AEH}\)= \(\widehat{BDH}\)(=90)
\(\widehat{AHE}\)= \(\widehat{BHD}\)( đối đỉnh)
=> \(\Delta\)AEH đồng dạng \(\Delta\)BDH
=> \(\frac{AH}{BH}=\frac{EH}{DH}\)
=> AH . DH = BH . EH (2)
Từ 1 và 2
=> AH.DH = BH.EH = CH.FH
ღᏠᎮღ๖ۣۜH ๖ۣۜH๖ۣۜU Đ๖ۣۜI❖ᵛᶰシ cop cc