Các câu hỏi tương tự
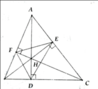
Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H ( D,E,F lần lượt thuộc các cạnh BC, CA, AB). CMR:a, AF.AB AH.AD AE.ACb, H là giao điểm 3 đường phân giác trong tam giác DEF.c, Gọi M,N,P,I,K,Q lần lượt là trung điểm của các cạnh BC, AC, AB, EF, ED, DF. CMR:các đường thẳng MI, NQ, PK đồng quyd, Gọi độ dài các đoạn thẳng AB, BC, CA lần lượt là a,b,c. Độ dài các đoạn thẳng AD, BE, CF là a, b, c. Tìm GTNN của biểu thức frac{left(a+b+cright)^2}{a^2+b^2+c^2}
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H ( D,E,F lần lượt thuộc các cạnh BC, CA, AB). CMR:
a, AF.AB = AH.AD = AE.AC
b, H là giao điểm 3 đường phân giác trong tam giác DEF.
c, Gọi M,N,P,I,K,Q lần lượt là trung điểm của các cạnh BC, AC, AB, EF, ED, DF. CMR:
các đường thẳng MI, NQ, PK đồng quy
d, Gọi độ dài các đoạn thẳng AB, BC, CA lần lượt là a,b,c. Độ dài các đoạn thẳng AD, BE, CF là a', b', c'. Tìm GTNN của biểu thức \(\frac{\left(a+b+c\right)^2}{a'^2+b'^2+c'^2}\)
Cho tam giác MNP vuông ở M, đường cao MH, phân giác góc MNP cắt MP tại D. Cho biết MN = 6cm, MP = 8cm. a) Tính NP. Chứng minh Δ H M N và Δ H P M đồng dạng. b) Trên NP lấy điểm E sao cho PE = 4cm. Chứng minh N E 2 = N H . N P c) Tính diện tích Δ P E D
1. Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh:a) H là giao điểm các đường phân giác trong tam giác DEF. b) Gọi M, N, P, Q, I, K lần lượt là trung điểm BC, CA, AB, EF, FD, DE. Chứng minh các đoạn thẳng MQ, NI, PK đồng quy.2. Cho tam giác ABC cân tại A có ABACb, BCa. Đường phân giác BD của tam giác ABC có độ dài bằng cạnh bên của tam giác. Chứng minh rằng 1/b−1/ab/(a+b)^2 ( dấu / là phân số, ^ là mũ).
Đọc tiếp
1. Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh:a) H là giao điểm các đường phân giác trong tam giác DEF. b) Gọi M, N, P, Q, I, K lần lượt là trung điểm BC, CA, AB, EF, FD, DE. Chứng minh các đoạn thẳng MQ, NI, PK đồng quy.
2. Cho tam giác ABC cân tại A có AB=AC=b, BC=a. Đường phân giác BD của tam giác ABC có độ dài bằng cạnh bên của tam giác. Chứng minh rằng 1/b−1/a=b/(a+b)^2 ( dấu / là phân số, ^ là mũ).
Cho ΔABC nhọn, các đường cao AD, BE, CF cắt nhau tại H.
a/ C/m ΔAEF và ΔABC đồng dạng.
b/ Gọi I là giao điểm của AD và EF. C/m IH.AD = AI.HD.
c/ Cho AB = 10cm; AC = 17cm; BC = 21cm. Tính \(S_{\text{Δ}ABC}\).
Cho Δ ABC có A = 80 độ , B = 60 độ
a, SS các cạnh của tg
b, Trên cạnh BC lấy điểm D sao cho BD = Ba . Tia phân giác của ABC cắt AC tại E
c, Cm : BE> AD
d , Gọi H là giao điểm của BE và AD . Cm : H là trung điểm của AD
Cho Δ ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và AC.
a) Chứng minh rằng: Δ AEF Δ ABC.
b) Cho AH = 4,8cm; BC = 10cm. Tính SΔAEF?
c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy tại một điểm.
cho tam giác ABC vuông tại B ( AB >AC). I là điểm đối xứng của C qua B. Từ I kẻ đường thẳng vuông góc với đoạn thẳng AC tại H; K là giao điểm của AB và IH. chứng minh:
a)Δ ABC ~Δ AHF
b) AB.KH=AH.BC
Cho tam giác ABC có ba góc nhọn, các điểm M, N thứ tự là trung điểm của BC và AC. Các đường trung trực của BC và AC cắt nhau tại O. Qua A kẻ đường thẳng song song với OM, qua B kẻ đường thẳng song song với ON, chúng cắt nhau tại Ha) Nối MN, Δ AHB đồng dạng với tam giác nào?b) Gọi G là trọng tâm Δ ABC, chứng minh Δ AHG đồng dạng với Δ MOG?c) Chứng minh ba điiểm M, O, G thẳng hàng?
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, các điểm M, N thứ tự là trung điểm của BC và AC. Các đường trung trực của BC và AC cắt nhau tại O. Qua A kẻ đường thẳng song song với OM, qua B kẻ đường thẳng song song với ON, chúng cắt nhau tại H
a) Nối MN, Δ AHB đồng dạng với tam giác nào?
b) Gọi G là trọng tâm Δ ABC, chứng minh Δ AHG đồng dạng với Δ MOG?
c) Chứng minh ba điiểm M, O, G thẳng hàng?
cho tam giác abc có 3 góc nhọn. các đường cao AD,BE,CF đồng quy tại H. M;N lần lượt là hình chiếu của B;C trên EF.
chứng minh AEF và ABC đồng dạng
chứng mính H cách đều 3 cạnh của tam giác DEF