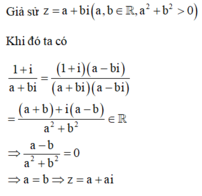
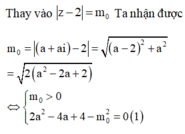
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a. Khi đó phương trình (1) phải thỏa mãn

Đáp án D
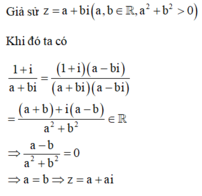
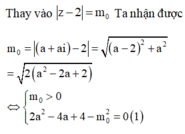
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a. Khi đó phương trình (1) phải thỏa mãn

Đáp án D
Cho số phức z thỏa mãn 1 + i z là số thực và z - 2 = m với m ∈ ℝ
Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán.
Khi đó
A. 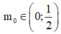
B. 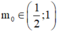
C. 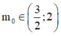
D. 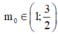
Cho số phức z thỏa mãn |z| = 1 m 2 + 2m, trong đó m là số thực dương tùy ý. Biết rằng với mỗi m, tập hợp các điểm biểu diễn số phức w = (2i+1)(i+ z ¯ )-5+3i là một đường tròn bán kính r. Tìm giá trị nhỏ nhất của r
A . 3 2
B . 2 3
C . 3 5
D . 5 3
Cho số phức z thỏa mãn z = i − m 1 − m m − 2 i , m ∈ ℝ là tham số và z . z ¯ = 1 5 . Khi đó số giá trị thỏa mãn là:
A. 2
B. 1
C. 0
D. 3
Có bao nhiêu giá trị nguyên của m để có đúng 2 số phức z thỏa mãn z - ( m - 1 ) + i = 8 và z - 1 + i = z - 2 + 3 i .
A. 130
B. 66
C. 65
D. 131
Cho hai số phức z, ω thỏa mãn z - 1 = z + 3 - 2 i ; ω = z + m + i với m ∈ ℝ là tham số. Giá trị của m để ta luôn có là
A. 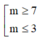
B. 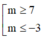
C. 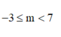
D. 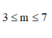
Cho số phức z thỏa mãn | ( z + 2 ) i + 1 | + | ( z ¯ - 2 ) i - 1 | = 10 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Tính tổng S=M+m.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn: |z+2+i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z-1-2i|. Tính S = M + m.
A. 6 2
B. 4 2
C. 2 2
D. 8 2
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z + i z , với z là số phức khác 0 thỏa mãn z ≥ 2 . Tính 2M-m
A. 2M-m = 3 2
B. 2M-m = 5 2
C. 2M-m = 10
D. 2M-m = 6
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = z + i z , với z là số phức khác 0 và thỏa mãn |z| ≥ 2. Tính 2M - m.
A. 2M - m = 3 2
B. 2M - m = 5 2
C. 2M - m = 10
D. 2M - m = 6