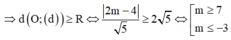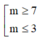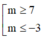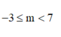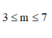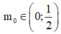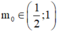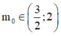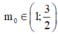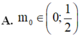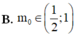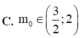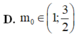Đáp án B
Ta có:

Tập hợp điểm M biểu diễn w là trung trực của ![]() nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
![]()
Đặt ![]()
Do ω ⩾ 2 5 nên M nằm ngoài đường tròn tâm O bán kính R= 2 5