Đáp án B
Phương pháp giải:
Tính diện tích hình phẳng giới hạn bởi 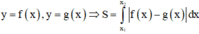
Lời giải:
Hoành độ giao điểm của (P1), (P2) là nghiệm phương trình:
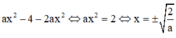
Khi đó, diện tích hình phẳng cần tính là
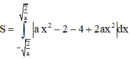
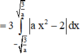
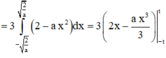
![]()
với 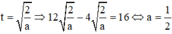
Đáp án B
Phương pháp giải:
Tính diện tích hình phẳng giới hạn bởi 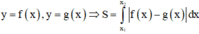
Lời giải:
Hoành độ giao điểm của (P1), (P2) là nghiệm phương trình:
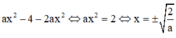
Khi đó, diện tích hình phẳng cần tính là
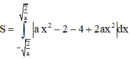
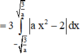
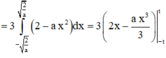
![]()
với 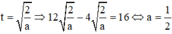
Cho a,b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol y = a x 2 và đường thẳng y = - b x . Thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc và giá trị của a và b nếu a và b thỏa mãn điều kiện sau
A. b 4 = 2 a 3
B. b 3 = a 5
C. b 4 = 2 a 2
D. b 5 = a 3
Cho a , b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol y = ax 2 và đường thẳng y = − b x . Thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc và giá trị của a và b nếu a và b thỏa mãn điều kiện sau
A. b 4 = 2 a 3
B. b 4 = 2 a 2
C. b 5 = a 3
D. b 3 = a 5
Gọi (H) là hình phẳng giới hạn bởi parabol (P): y = 8 x - x 2 và trục hoành. Các đường thẳng y=a,y=b,y=c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức ( 16 - a ) 3 + ( 16 - b ) 3 + ( 16 - c ) 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.
Cho parabol (P): y = x 2 và đường thẳng d đi qua điểm A(1;2). Diện tích hình phẳng giới hạn bởi (C) và d có giá trị nhỏ nhất bằng
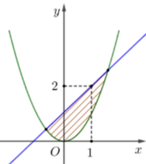
A. 3 4
B. 1 + 2 2
C. 4 3
D. 2
Cho a, b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol y = a x 2 và đường thẳng y = - b x . Thể tích khối tròn xoay tạo được khi quay K quanh trục hoành là một số không phụ thuộc vào giá trị của a và b nếu a và b thỏa mãn diều kiện nào sau đây?
A. b 4 = 2 a 2
B. b 4 = 2 a 5
C. b 5 = 2 a 3
D. b 3 = 2 a 5
Diện tích hình phẳng giới hạn bởi các đường x=-1; x=2; y=0 và parabol P : y = a x 2 + b x + c bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Tính T=a+b-c
A. T = -8.
B. T = -2.
C. T = 14.
D. T = 3.
Diện tích hình phẳng giới hạn bởi các đường x = − 1 , x = 2 , y = 0 và Parabol ( P ) : y = a x 2 + b x + c bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu?
A. -8
B. -2
C. 14
D. 3
Trong hệ trục tọa độ Oxyz, cho Parabol P : y = x 2 và hai đường thẳng y = a , y = b 0 < a < b (hình vẽ). Gọi S 1 là diện tích hình phẳng giới hạn bởi parabol (P) đường thẳng y = a và đường thẳng y = b (phần gạch chéo) và S 2 là diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng y = a (phần tô đậm). Với điều kiện nào sau đây của a và b thì S 1 = S 2
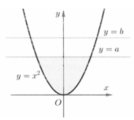
A. b = 4 a 3
B. b = 2 a 3
C. b = 3 a 3
D. b = 6 a 3
Cho Parabol P : y = x 2 và hai điểm A, B thuộc P sao cho A B = 2 . Diện tích hình phẳng giới hạn bởi P và đường thẳng AB đạt giá trị lớn nhất bằng bao nhiêu?
A. 4 3
B. 5 3
C. 2 3
D. 5 4