Chọn đáp án D
Hình chóp S.ABCD có 5 mặt nên thiết diện của hình chóp có tối đa 5 cạnh. Vậy thiết diện không thể là lục giác
Chọn đáp án D
Hình chóp S.ABCD có 5 mặt nên thiết diện của hình chóp có tối đa 5 cạnh. Vậy thiết diện không thể là lục giác
Cho hình chóp S . A B C D có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng ( S A B ) , ( S B C ) , ( S C D ) , ( S D A ) với mặt đáy lần lượt là 90 ° , 60 ° , 60 ° , 60 ° . Biết rằng tam giác SAB vuông cân tại S , A B = a và chu vi tứ giác ABCD là 9a. Tính thể tích V của khối chóp S . A B C D ?
A. V = a 3 3 4
B. V = a 3 3
C. V = 2 a 3 3 9
D. V = a 3 3 9
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành?
A. AB = 3CD
B. AB = 2CD
C. CD = 2AB
D. CD = 3AB
Cho khối chóp tứ giác S.ABCD có đáy ABCD là hình thoi và SABC là tứ diện đều cạnh a. Thể tích V của khối chóp S.ABCD là
A. V = 2 2 a 3
B. V = 2 6 a 3
C. V = 2 4 a 3
D. V = 2 12 a 3
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a, S A ⊥ A B C D và SA=3a. Thể tích của khối chóp S.ABCD là
A. V = a 3
B. V = 6 a 3
C. V = 3 a 3
D. V = 2 a 3
Cho hình chóp S.ABCD có đáy là tứ giác lồi hai đường chéo AC và BD vuông góc với nhau, mặt bên SAD là tam giác đều, AD=4,AC=6,BD=8. Thể tích của khối chóp S.ABCD bằng 24. Góc giữa hai mặt phẳng (SAD) và (ABCD) bằng
A. 60 °
B. 30 °
C. 45 °
D. 90 °
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a, S A ⊥ A B C , S A = 3 a . Thể tích V của khối chóp S.ABCD là
A. V = 2 a 3
B. V = 3 a 3
C. V = 1 3 a 3
D. V = a 3
Hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông cân tại S và tam giác SCD đều. Tính bán kính mặt cầu ngoài tiếp hình chóp S.ABCD.
A. R = a 2
B. R = a 7 12
C. R = a 3
D. R = a 3 4
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a và S A ⊥ ( A B C ) , SA=3a. Thể tích V của khối chóp S.ABCD là
A. a 3
B. 3 a 3
C. 1 3 a 3
D. 2 a 3
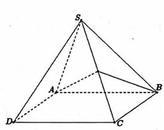
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo thiết diện có chu vi bằng 7a (tham khảo hình vẽ bên). Thể tích của khối nón có đỉnh là S và đường tròn ngoại tiếp tứ giác ABCD bằng:
A. 2 6 9 πa 3
B. 6 3 πa 3
C. 2 3 3 πa 3
D. 2 6 3 πa 3