a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0 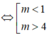
Do x1 < x2 < 1
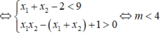
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0 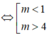
Do x1 < x2 < 1
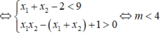
Cho phương trình \(x^2-2\left(m+1\right)x+m^2+2m=0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1,x2(x1<x2)
thoa man: \(\left|x1\right|=3\left|x2\right|\)
Cho phương trình m x 2 + ( m 2 - 3 ) x + m = 0 . Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm x 1 ; x 2 thỏa mãn x 1 + x 2 = 13 4 . Khi đó tổng bình phương các giá trị tìm được của tham số m bằng:
A. 265 16
B. 16
C. 9 16
D. 73 16
Cho phương trình: x2-(2m-1)x+m-1=0
a) chứng minh rằng phương trình luôn cố 2 nghiệm phân biệt x1,x2 với mọi m
b) tìm tất cẩ các giá trị của m để x13+x23=2m2-m
Cho phương trình x 2 - m - 1 x + m + 4 = 0 .Giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn x 1 - x 2 = 1 là:
![]()
![]()
![]()
![]()
Cho phương trình 2 x 2 + 2 m - 1 x + m 2 - 1 = 0 . Tìm giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn biểu thức A = x 1 - x 2 2 đạt giá trị lớn nhất.
![]()
![]()
![]()
![]()
Cho phương trình x 2 - 2 m + 1 x + 2 m 2 - 2 = 0 Tìm giá trị của m để phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn biểu thức A = x 1 2 + x 2 2 + x 1 x 2 đạt giá trị nhỏ nhất.
A. m=1
B. Không tồn tại m.
C. m=-2
D. Có vô số giá trị m.
Tất cả các giá trị của m để phương trình x^2−2(2m−3)x+4m−3 = 0 có hai nghiệm x1,x2 thỏa mãn điều kiện x1+x2−2x1x2 < 8 là gì?
Online chờ gấp, đa tạ các vị!
Tìm tất cả các giá trị của tham số m để phương trình x^2+2x+m=0 có hai nghiệm x1, x2 thỏa mãn \(\dfrac{x_1^2-3_{x_1}+m}{x_2}+\dfrac{x_2^2-3_{x_2}+m}{x_1}\le2\)