Question

Cho nửa đường tròn tâm O đường kính AB Gọi C, D thuộc nữa đường tròn ( C thuộc cung AD) AD cắt BC tại H, AC cắt BD tại E
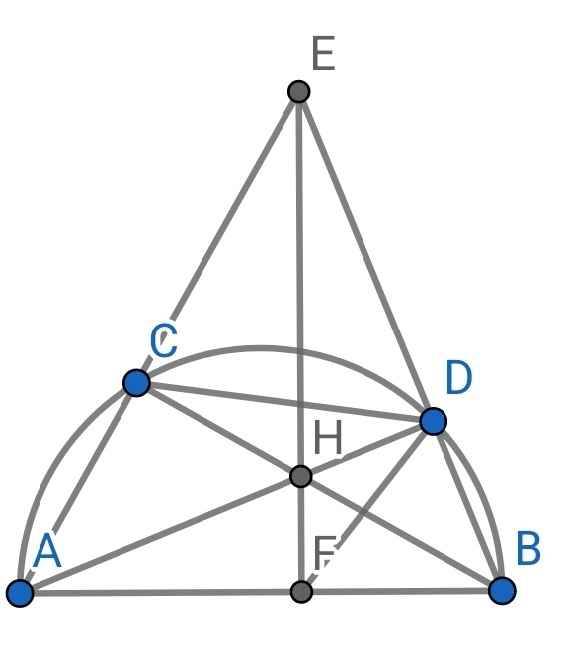
vẽ EH cắt  AB tại E.C/M DA là phân giác của góc CDF

Answer 1

  Sửa đề: EH cắt AB tại F

Ta có:

∠ACB = ∠ADB = 90⁰ (góc nội tiếp chắn nửa đường tròn)

Tứ giác ABDC có:

∠ACB = ∠ADB = 90⁰ (cmt)

⇒ C, D cùng nhìn AB dưới một góc 90⁰

⇒ ABDC nội tiếp

⇒ ∠ABC = ∠ADC (hai góc nội tiếp cùng chắn cung AC) (1)

Do ∠ACB = 90⁰ (cmt)

⇒ BC ⊥ AE

⇒ BC là đường cao của ∆EAB

Do ∠ADB = 90⁰ (cmt)

⇒ AD ⊥ BE

⇒ AD là đường cao của ∆EAB

Mà H là giao điểm của AD và BC

⇒ EH là đường cao thứ ba của ∆EAB

⇒ EF ⊥ AB

⇒ ∠HFB = 90⁰

Xét tứ giác BDHF có:

∠HDB = ∠HFB = 90⁰

⇒ ∠HDB + ∠HFB = 90⁰ + 90⁰ = 180⁰

⇒ BDHF nội tiếp

⇒ ∠HDF = ∠HBF (hai góc nội tiếp cùng chắn cung HF)

⇒ ∠ADF = ∠ABC (2)

Từ (1) và (2) ⇒ ∠ADF = ∠ADC

⇒ DA là tia phân giác của ∠CDF