Đáp án D
Ta có ![]()
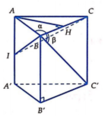
Gọi H là trung điểm của BC.
∆ AHB vuông tại H
![]()
![]()
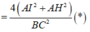
Mà
∆
BIC vuông tại I![]()
Thay vào (*) ta có: tan 2 α + tan 2 β = 1
Đáp án D

Ta có ![]()
Gọi H là trung điểm của BC.
∆ AHB vuông tại H
![]()
![]()
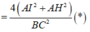
Mà
∆
BIC vuông tại I![]()
Thay vào (*) ta có: tan 2 α + tan 2 β = 1
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân đỉnh A, A B C ^ = α , BC' tạo với (ABC) góc β . Gọi I là trung điểm AA', biết B I C ^ = 90 0 . Tính tan 2 α + tan 2 β
A . 1 2
B . 2
C . 3
D . 1
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB = AC = a; BAC=120º và AA’ = a. Gọi I là trung điểm của CC' (như hình vẽ). Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và (AB’I).
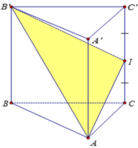

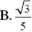
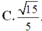
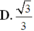
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc α là góc giữa hai đường thẳng AA’ và BM
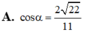
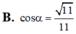
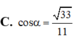
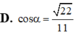
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AC = 2, BC = 1, AA' = 1. Tính góc giữa AB' và (BCC'B')
Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy là một tam giác vuông cân tại B, AB = BC = a, AA' = a 2 , M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM và B'C
A . a 7
B . a 3 2
C . 2 a 5
D . a 3
Cho hình lăng trụ đứng ABC.A'B'C' đáy ABC là tam giác đều, I là trung điểm của AB. Kí hiệu d(AA',BC) là khoảng cách giữa 2 đường thẳng AA' và BC thì:
A. d(AA',BC) = AB
B. d(AA',BC) = IC
C. d(AA',BC) = A'B
D. d(AA',BC) = AC
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = BC = a, cạnh bên A A ' = a 2 . Gọi M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM, B'C.
Cho lăng trụ tam giác ABC.A' B' C' có đáy là tam giác vuông cân tại A,AA' = a 3 hình chiếu vuông góc của A’ lên (ABC) là trung điểm cạnh AC. Biết góc giữa AA' và mặt phẳng (ABC) bằng 45 0 . Thể tích của khối lăng trụ ABC.A' B' C' là:
A. a 3 6
B. a 3 3 4
C. 3 a 3 6 2
D. a 3 6 3
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B, BC = 2a, A’M = 3a với M là trung điểm cạnh BC. Thể tích khối lăng trụ ABC.A'B'C' là
A. 8 a 3 3
B. 8 a 3 3
C. 16 a 3 3 3
D. 4 a 3