Đáp án A
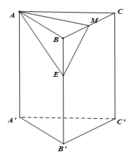
Gọi E là trung điểm của BB' => ME//B'C => (AME)//B'C
![]() = d(C;(AME))
= d(C;(AME))
Vì ![]()
![]()
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên :
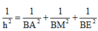
![]()
Đáp án A

Gọi E là trung điểm của BB' => ME//B'C => (AME)//B'C
![]() = d(C;(AME))
= d(C;(AME))
Vì ![]()
![]()
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên :
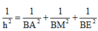
![]()
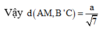
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông với AB = BC = a, cạnh bên A A ' = a 2 . Gọi M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM, B'C.
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, AC =a 3 và BB'C'C là hình vuông. Khoảng cách giữa hai đường thẳng AA' và BC' là
A. a 3 2
B. 3 a 2 4
C. a
D. a 3
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông BA = BC = a, cạnh bên AA' = a 2 . M là trung điểm của BC. Khoảng cách giữa AM và B'C là:
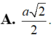
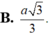
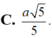
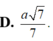
Cho hình lăng trụ đứng ABC.A’B’C’có đáy là tam giác vuông và AB=BC=a, AA'= a 2 . Gọi M là trung điểm của BC. Tính khoảng cách d của hai đường thẳng AM và B’C
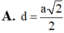
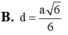
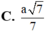
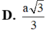
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông ở A, AB=2a AC=a, AA'=4a M là điểm thuộc cạnh AA' sao cho MA'=3MA . Tính khoảng cách giữa hai đường chéo nhau BC và C'M
![]()
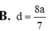
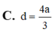

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, BA=BC=a, cạnh bên A A ' = a 2 , M là trung điểm của BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng
A. a 2 2
B. a 3 3
C. a 5 5
D. a 7 7
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy là ABC là tam giác vuông BA = BC =a, cạnh bên A A ' = a 2 .Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM, B’C’.
![]()
![]()
![]()
![]()
Cho hình lăng trụ đứng ABC.A'B'C', đáy ABC là tam giác vuông tại A, cạnh AA' hợp với B'C một góc 60 0 và khoảng cách giữa chúng bằng a, B'C = 2a. Thể tích của khối lăng trụ ABC.A'B'C' theo a
A . a 3 2
B . 3 a 3 2
C . 3 a 3 4
D . a 3 4
Cho hình lăng trụ đứng ABC.A'B'C' đáy ABC là tam giác đều, I là trung điểm của AB. Kí hiệu d(AA',BC) là khoảng cách giữa 2 đường thẳng AA' và BC thì:
A. d(AA',BC) = AB
B. d(AA',BC) = IC
C. d(AA',BC) = A'B
D. d(AA',BC) = AC