Đáp án A
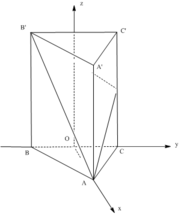
Gắn hệ trục tọa độ Oxyz như hình vẽ
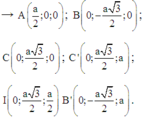
Vecto pháp tuyến của mặt phẳng
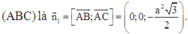
Vecto pháp tuyến của mặt phẳng (AB’I) là
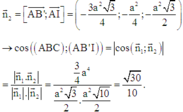
Đáp án A

Gắn hệ trục tọa độ Oxyz như hình vẽ
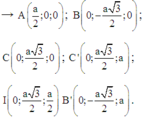
Vecto pháp tuyến của mặt phẳng
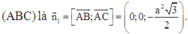
Vecto pháp tuyến của mặt phẳng (AB’I) là
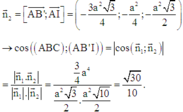
Cho lăng trụ đứng ABC.A'B'C' có cạnh bên AA' = 2a, AB = AC = a, góc B A C ^ = 120 0 . Gọi M là trung điểm của BB' thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC'M) là:
A . 3 31
B . 5 5
C . 3 15
D . 93 31
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc α là góc giữa hai đường thẳng AA’ và BM
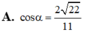
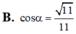
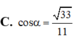
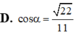
Cho hình lăng trụ đứng ABC.A'B'C' có AA' = AB =AC =1 và B A C ^ = 120 o Gọi I là trung điểm cạnh CC' Côsin góc giữa hai mặt phẳng (ABC) và (AB'I) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
Cho hình lăng trụ đứng ABC.A'B'C' có AA' = AB = AC =1 B A C ^ = 120 o Gọi M là trung điểm cạnh CC′. Côsin góc giữa hai mặt phẳng (ABC) và (AB′M) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
Cho lăng trụ đứng ![]() . Gọi I là trung điểm của CC' . Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và (AB'I).
. Gọi I là trung điểm của CC' . Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và (AB'I).
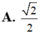
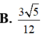
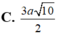
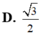
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân ABC với AB=AC=a,BAC= 120 o mặt phẳng (AB'C') tạo với đáy một góc 30 o Tính thể tích V của khối lăng trụ đã cho.
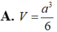
![]()
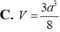
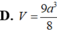
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác ABC đều cạnh a . Gọi I là trung điểm AB , hình chiếu của điểm A' lên (ABC ) là trung điểm H của đoạn CI , góc giữa đường thẳng AA' và mặt phẳng (ABC ) bằng 45 độ. Tính khoảng cách giữa hai đường thẳng chéo nhau A A' và CI
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân đỉnh A, A B C ^ = α , BC' tạo với (ABC) góc β . Gọi I là trung điểm AA', biết B I C ^ = 90 0 . Tính tan 2 α + tan 2 β
A . 1 2
B . 2
C . 3
D . 1
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân đỉnh A, A B C ^ = α , BC' tạo với (ABC) góc β . Gọi I là trung điểm AA', biết B I C ^ = 90 0 . Tính tan 2 α + tan 2 β
A . 1 2
B . 2
C . 3
D . 1