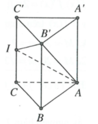
HD: Dễ thấy ABC là hình chiếu vuông góc của AB’I trên (ABC)
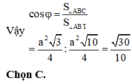

HD: Dễ thấy ABC là hình chiếu vuông góc của AB’I trên (ABC)
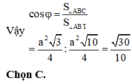
Cho lăng trụ đứng cóABC.A'B'C' có A B = A C = B B ' = a , B A C = 120 ° . Gọi I là trung điểm của CC'. Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và (AB'I).
A. 2 2
B. 3 5 12
C. 30 10
D. 3 2
Cho lăng trụ đứng A B C . A ' B ' C ' có A B = A C = B B ' = a , B A C ^ = 120 ° . A B C Gọi I là trung điểm của CC’. Ta có cosin của góc giữa hai mặt phẳng A B C và A B ' I bằng:
A. 3 2
B. 30 10
C. 3 5 12
D. 2 2
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác cân với A B = A C = a và góc B A C = 120 ° , cạnh bên B B ' = a ,gọi I là trung điểm của CC'. Côsin góc tạo bởi mặt phẳng (ABC) và (AB'I) bằng.
A. 20 10
B. 30
C. 30 10
D. 30 5
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác cân, A B = A C = a , B A C ^ = 120 ° ,
B B ' = a , I là trung điểm của CC'. Gọi α là góc giữa hai mặt phẳng A B C và A B ' I . Tính cos α
A. cos α = 3 10
B. cos α = 3 10
C. cos α = 3 10
D. cos α = 2 5
Cho hình lăng trụ đứng ABC.A' B' C' có AB=AC=a, góc ∠ BAC = 120 0 , AA ' = a .Gọi M, N lần lượt là trung điểm của B^' C^' và CC^'. Số đo góc giữa mặt phẳng (AMN) và mặt phẳng (ABC) bằng:
A. 60 0
B. 30 0
C. arcsin 3 4
D. arccos 3 4
Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân, AB = AC = a, BAC = 120 ° BB' = a, I là trung điểm CC'. Gọi α là góc giữa hai mặt phẳng (ABC) và (AB'I). Tính cos α
A. c o s α = 3 10
B. c o s α = 3 10
C. c o s α = 3 10
D. c o s α = 3 5
Cho lăng trụ đứng ABC.A'B'C' có cạnh bên AA'=2a,AB=AC =a, góc B A C ^ = 120 ° . Gọi M là trung điểm của BB' thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC'M) là:
A. 3 31
B. 5 5
C. 3 15
D. 93 31
Cho hình lăng trụ đứng ABC. A 'B 'C ' có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm của AB. Cho biết A B = 2 a ; B C = 13 ; C C ' = 4 a . Khoảng cách giữa hai đường thẳng A 'B và CE bằng
A. 4 a 7
B. 12 a 7
C. 6 a 7
D. 3 a 7
Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AB=3; AC=4và A A ' = 61 2 Hình chiếu của B’ lên mặt phẳng (ABC) là trung điểm cạnh BC, điểm M là trung điểm A’B’ Tính cosin của góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) bằng:
A. 11 3157
B. 13 65
C. 33 3517
D. 33 3157