Chọn đáp án A
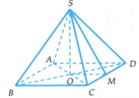
Gọi O là tâm của hình vuông ABCD, suy ra S O ⊥ A B C D
Gọi M là trung điểm của CD thì C D ⊥ O M mà C D ⊥ O M ⇒ C D ⊥ S O M
Đặt AB = 2x(x > 0) ⇒ O M = x
Do ∆ S O M vuông tại O nên S O = O M . tan S M O ⏜ = x . tan α
Do ∆ S O A vuông tại O nên S A 2 = S O 2 + O A 2
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 S O . S A B C D
Ta có
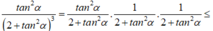
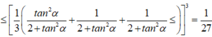
Suy ra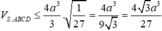 
Dấu “=” xảy ra khi
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh AB = a (a>0) Góc giữa mặt bên và mặt đáy bằng 60 ° Tính thể tích khối chóp S.ABCD:
A. a 3 3 2
B. a 3 6
C. a 3 3 3
D. a 3 3 6
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC.
Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính
góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = arcsin 1 + 33 8
B. φ = arcsin 33 − 1 8
C. φ = arcsin 1 + 29 8
D. φ = arcsin 29 − 1 8
Cho khối chóp tứ giác đều S.ABCD có thể tích bằng a 3 và đáy ABCD là hình vuông cạnh a. Tính cosα với α là góc giữa mặt bên và mặt đáy
A. cos α = 1 5
B. cos α = 1 3
C. cos α = 1 37
D. cos α = 1 19
Cho hình chóp S.ABCD có các cạnh bên bằng a, góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng α ( α thay đổi). Tìm giá trị lớn nhất của thể tích của S.ABCD?
A. 2 a 3 3 3
B. 2 a 3 9 3
C. 4 a 3 3 3
D. Đáp án khác
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân (AD//BC), BC=2a, AB=AD=DC=a với a>0. Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và BD. Biết SD vuông góc AC. M là một điểm thuộc đoạn OD; MD=x với x>0; M khác O và D. Mặt phẳng (α) đi qua (α) đi qua M và song song với hai đường thẳng SD và AC cắt khối chóp S.ABCD theo một thiết diện. Tìm x để diện tích thiết diện là lớn nhất?
A. a 3 4
B. a 3
C. a 3 2
D. a
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x 0 < x < α . Mặt phẳng α qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60 ° . Tính theo a thể tích khối chóp S.ABCD
A. V = a 3 6 6
B. V = a 3 6 2
C. V = a 3 6 3
D. V = a 3 3
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh, a góc giữa mặt bên và mặt phẳng đáy là α thoả mãn cos α = 1 3 . Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị nào trong các giá trị sau
A. 0,11
B. 0,13
C. 0,7
D. 0,9
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, góc giữa mặt bên và mặt phẳng đáy là α thỏa mãn cos α = 1 3 . Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỷ số thể tích của hai khối đa diện (khối bé chia khối lớn) bằng
A. 1 9
B. 1 10
C. 7 9
D. 9 10
