Thể tích vật thể khi quay hình vuông OABC quanh trục Ox là ![]()
Thể tích vật thể khi quay phần gạch sọc quanh Ox là 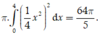
Vậy thể tích vật thể tròn xoay cần tính bằng 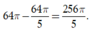
Chọn D.
Thể tích vật thể khi quay hình vuông OABC quanh trục Ox là ![]()
Thể tích vật thể khi quay phần gạch sọc quanh Ox là 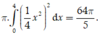
Vậy thể tích vật thể tròn xoay cần tính bằng 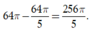
Chọn D.
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ).
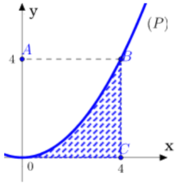
Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
A. V = 128 π 5
B. V = 128 π 3
C. V = 64 π 5
D. V = 256 π 5
Cho hình phẳng (D) được giới hạn bởi các đường x = 0 , x = π , y = 0 và y = − sin x . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
A. V = π ∫ 0 π sin x d x .
B. V = π ∫ 0 π sin 2 x d x .
C. V = π ∫ 0 π − sin x d x .
D. V = ∫ 0 π sin 2 x d x .
Cho hình phẳng (D) giới hạn bởi các đường: y = x - π ; y = sinx ; x = 0 . Gọi V là thể tích khối tròn xoay tạo thành do (D) quay quanh trục hoành và V = p π 4 p ∈ ℚ . Giá trị của 24p bằng:
A. 8
B. 4
C. 24
D. 12
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x cung tròn có phương trình y = 6 - x 2 ( 6 ≤ x ≤ 6 ) và trục hoành (phần gạch chéo trong hình vẽ). Tính thể tích V của vật thể xoay tròn sinh bởi hình phẳng D khi quay D quanh trục Ox.
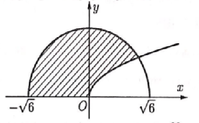
A. V = 8 π 6 - 2 π .
B. V = 8 π 6 + 22 π 3 .
C. V = 8 π 6 - 22 π 3 .
D. V = 4 π 6 + 22 π 3 .
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y =sinx.cosx, trục tung, trục hoành và đường thẳng x =π/2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V =π/16.
B. V = π 2 16
C. V = π 2 + π 16
D. V = π 2 4
Cho hình phẳng (H) giới hạn bởi đường cong y = ln x , trục hoành, đường thẳng x = 1 và x = k k > 1 . Gọi V k là thể tích khối tròn xoay thu được khi quay hình (H) quay quanh trục Ox. Biết rằng V k = π . Hãy chọn khẳng định đúng?
A. 3 < k < 4
B. 1 < k < 2
C. 2 < k < 3
D. 4 < k < 5
Cho hình trụ có diện tích xung quanh bằng 4 π , thiết diện qua trục là hình vuông. Tính thể tích V của khối trụ giới hạn bởi hình trụ
A. V = 2 π
B. V = 6 π
C. V = 3 π
D. V = 5 π
Gọi D là diện tích hình phẳng giới hạn bởi các đường y = sin 2 x , trục tung, trục hoành và đường thẳng x = π . Quay hình phẳng D quay trục Ox ta được khối tròn xoay có thể tích là
A. π 2 .
B. π 2 .
C. π 2 4 .
D. π 2 2 .
Cho hai hình vuông có cạnh đều bằng 5 được xếp lên nhau sao cho đỉnh M của hình vuông này là tâm của hình vuông kia, đường chéo MN vuông góc với cạnh PQ tạo thành hình phẳng (H) ( như hình vẽ bên).
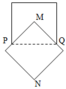
Tính thể tích V của vật thể tròn xoay khi quanh hình (H) quanh trục MN.
A. V = 125 ( 1 + 2 ) π 6
B. V = 125 ( 5 + 2 2 ) π 12
C. V = 125 ( 5 + 4 2 ) π 24
D. V = 125 ( 2 + 2 ) π 4