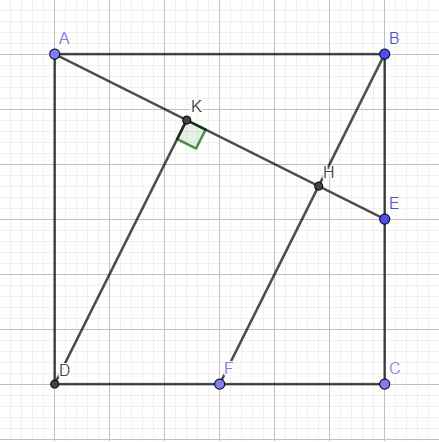
a. Dễ dàng chứng minh hai tam giác vuông ABE và BCF bằng nhau (c.g.c)
\(\Rightarrow\widehat{AEB}=\widehat{BFC}\)
Mà \(\widehat{AEB}+\widehat{AEC}=180^0\Rightarrow\widehat{BFC}+\widehat{AEC}=180^0\)
\(\Rightarrow\widehat{EHF}=360^0-\left(\widehat{C}+\widehat{BFC}+\widehat{AED}\right)=90^0\)
Hay \(AE\perp BF\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ABE:
\(AB^2=AH.AE\Rightarrow AH=\dfrac{AB^2}{AE}\Rightarrow\dfrac{AH}{AE}=\dfrac{AB^2}{AE^2}=\dfrac{AB^2}{AB^2+BE^2}=\dfrac{AB^2}{AB^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{4}{5}\)
\(\dfrac{BH}{BF}=\dfrac{BH}{AE}=\dfrac{\dfrac{AB.BE}{AE}}{AE}=\dfrac{AB.BE}{AE^2}=\dfrac{AB.\dfrac{1}{2}AB}{AB^2+\left(\dfrac{1}{2}AB\right)^2}=\dfrac{2}{5}\)
c. Hai tam giác vuông ABH và DAK đồng dạng (\(\widehat{ADK}\) và \(\widehat{BAH}\) cùng phụ \(\widehat{DAK}\))
\(\Rightarrow\dfrac{AK}{AD}=\dfrac{BH}{AB}\Rightarrow AK=\dfrac{AD.BH}{AB}=BH\)
Mà \(tan\widehat{BAH}=\dfrac{BH}{AH}=\dfrac{BE}{AB}=\dfrac{1}{2}\Rightarrow BH=\dfrac{1}{2}AH\)
\(\Rightarrow AK=\dfrac{1}{2}AH\) hay K là trung điểm AH