Đáp án D
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
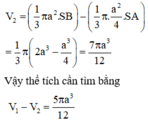
Đáp án D

Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
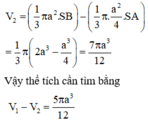
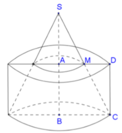
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD. Xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường thẳng AB. Thể tích của khối tròn xoay đó bằng
A. 5 πa 3 12
B. 3 πa 3 4
C. 7 πa 3 12
D. πa 3 3
Cho hình phẳng D giới hạn bởi đường cong y = 3 + x − 2 e x x e x + 1 , trục hoành và hai đường thẳng x=0, x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V = π a + b ln 1 + 1 e , trong đó a, b là các số hữu tỷ. Mệnh đề nào dưới đây là đúng?
A. a+b=5
B. a-2b=5
C. a+b=3
D. a-2b=7
Cho tam giác ABC đều cạnh 3 và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm (hình vẽ bên) quay quanh đường thẳng AD bằng
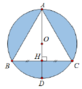
A. V = 9 3 8 π
B. V = 23 3 8 π
C. V = 23 3 24 π
D. V = 5 3 8 π
Cho tứ diện ABCD có A D ⊥ A B C , ABC là tam giác vuông tại B. Biết B C = a , A B = a 3 , A D = 3 a . Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
A. 3 3 π a 3 16
B. 8 3 π a 3 3
C. 5 3 π a 3 16
D. 4 3 π a 3 16
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Cho tam giác vuông có hai cạnh góc vuông là a và b. Quay tam giác đó (cùng với phần trong của nó) quanh đường thẳng chứa cạnh huyển, ta được một khối tròn xoay có thể tích bằng
A. π a 2 b 2 3 a 2 + b 2
B. π 3 b 2 a 2 + b 2
C. π a 2 b 2 3 a + b
D. π 3 a b a 2 + b 2
Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.
A. V = 17 π
B. V = 5 π
C. V = 15 π
D. V = 30 π
Cho tam giác ABC có AB = 3,BC = 5,CA = 7. Tính thể tích của khối tròn xoay sinh ra là do hình tam giác ABC quay quanh đường thẳng AB:
A. 50 π
B. 75 π 4
C. 275 π 8
D. 125 π 8
Cho một hình thang cân ABCD có cạnh đáy A B = 2 a , C D = 4 a , cạnh bên A D = B C = 3 a . Hãy tính thể tích của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó.
A. 4 2 π a 3 3
B. 56 2 π a 3 3
C. 16 2 π a 3 3
D. 14 2 π a 3 3